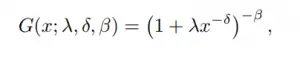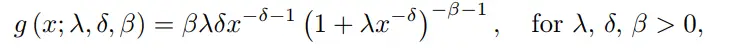Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 13 de marzo de 2022, por Luis Benites.
Conclusiones clave:
- La distribución Dagum es una forma de modelar la distribución de la riqueza.
- Cuando se aplica a datos empíricos, el Dagum supera las distribuciones de Pareto y lognormal.
- Las opciones incluyen variantes de tres y cuatro parámetros.
La distribución de Dagum (también llamada distribución de Burr inversa ; Dagum la llamó distribución de Burr logística generalizada ) fue propuesta por Camilo Dagum en la década de 1970 para modelar el ingreso y la riqueza.
Dagum desarrolló los modelos como una alternativa a la distribución de Pareto y la distribución lognormal , que, en su opinión, no dieron como resultado modelos precisos cuando se aplicaron a la distribución de ingresos. Más específicamente, Dagum no estaba satisfecho con la forma en que Pareto y lognormal manejan los datos de cola pesada . Específicamente, sintió que se podría desarrollar un mejor modelo para las colas pesadas que a menudo se encuentran en las distribuciones empíricas de ingresos y riqueza, al tiempo que permite un modo interior . El Pareto maneja bien las colas pesadas, pero el lognormal no. Y mientras que el lognormal permite un modo interior (o un modo en cero), Pareto no lo permite. La distribución de Dagum permite un modo interior y maneja colas pesadas (Kleiber, 2007).
A pesar de su relativa impopularidad, la distribución de Dagum a menudo funciona mejor que otros modelos de distribución de ingreso/riqueza de dos o tres parámetros cuando se aplica a datos empíricos .
CDF y PDF de distribución de Dagum
La CDF de la distribución Dagum Tipo I (tres parámetros) es: La PDF es: Donde:


- λ = un parámetro de escala ,
- δ y Β = parámetros de forma .
Cuando Β = 1, la distribución se denomina distribución log-logística .
Tipos
La distribución Dagum Tipo I de tres parámetros evolucionó a partir de la experimentación de Dagum con una distribución log-logística desplazada (Chotikapanich, 2008). También se desarrollaron dos generalizaciones de cuatro parámetros (Tipo II).
Referencias
Atkinson, A. (2014). Manual de Distribución del Ingreso, Volumen 2 . Elsevier.
Chotikapanich, D. (Ed.) (2008). Modelado de distribuciones de ingresos y curvas de Lorenz . Springer Science & Business Media.
Dagum, C., A New Model of Personal Income Distribution: Specification and Estimation,
Economie Applique’e, 30, 413 – 437, (1977).
Kleiber, C. y Kotz, S. (2003). Distribuciones estadísticas de tamaño en economía y ciencias actuariales. John Wiley & Sons.
Kleiber, C. (2007). Una guía para las distribuciones de Dagum. Recuperado el 26 de mayo de 2020 de: http://citeseerx.ist.psu.edu/viewdoc/download;jsessionid=BEE8C9083715B6042596B0DC170BFDA1?doi=10.1.1.610.8346&rep=rep1&type=pdf¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:
La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo: