Actualizado por ultima vez el 30 de septiembre de 2021, por Luis Benites.
¿Qué es una distribución Tweedie?
La distribución de Tweedie es un caso especial de una distribución exponencial . Puede tener un grupo de elementos de datos en cero (llamado «masa puntual»), que es particularmente útil para modelar reclamos en la industria de seguros, en pruebas médicas/genómicas o en cualquier otro lugar donde haya una combinación de ceros y no negativos. puntos de datos. Básicamente, si ve un histograma con un pico en cero, es un posible candidato para ajustarse a un modelo Tweedie.
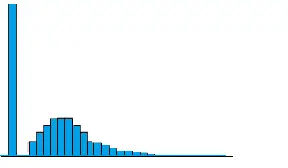
La distribución Tweedie tiene una masa puntual en cero antes de seguir una curva exponencial «regular».
La distribución de Tweedie es en realidad una familia de distribuciones que son un subconjunto de los modelos de dispersión exponencial (EDM). Los EDM son distribuciones de dos parámetros de la familia exponencial lineal que tienen un parámetro de escala φ.
Media, varianza y forma
Esta familia de distribuciones tiene las siguientes características:
La p en la función de varianza es un parámetro de forma adicional para la distribución. “p” a veces se escribe en términos del parámetro de forma α:
p = (α – 2) / (α -1).
Algunas distribuciones familiares son casos especiales de la distribución Tweedie:
- p = 0 : Distribución normal,
- p = 1: distribución de Poisson,
- 1 < p < 2: Distribución compuesta de Poisson/gamma,
- p = 2 distribución gamma ,
- 2 < p < 3 Distribuciones estables positivas,
- p = 3: distribución gaussiana inversa / distribución de Wald ,
- p > 3: distribuciones estables positivas,
- p = ∞ Distribuciones extremadamente estables.
La distribución no está definida para valores de “p” de 0 a 1.
La función de densidad de probabilidad para la familia Tweedie es compleja y no se puede expresar de forma cerrada simple (pero a veces se expresa como una serie de funciones). Como la distribución imita otras distribuciones para algunos valores de «p», puede usar el pdf para esas funciones. Por ejemplo, si p es 3, puede usar el pdf para el gaussiano inverso.
Referencias :
Tweedie, MCK (1984). Un índice que distingue entre algunas familias exponenciales importantes. En Estadística: Aplicaciones y Nuevas Direcciones. Actas de la Conferencia Internacional del Jubileo de Oro del Instituto de Estadística de la India. (Eds. JK Ghosh y J. Roy), págs. 579-604. Calcuta: Instituto de Estadística de la India.
Referencias
Kotz, S.; et al., editores. (2006), Enciclopedia de Ciencias Estadísticas , Wiley.

