Actualizado por ultima vez el 5 de febrero de 2022, por Luis Benites.
El término “distribución Euleriana” puede referirse a:
- Una distribución utilizada en las estadísticas de permutación para contar los descensos, o
- Una distribución Tipo III (p/q, p).
Distribución Euleriana en Estadísticas de Permutación
En las estadísticas de permutación, la distribución Euleriana es el nombre clásico para la distribución de las estadísticas de descendencia. Un descenso en una permutación α1, α2, …, αn es un índice I para el cual αi > αi+1 [1]. El número euleriano cuenta el número de permutaciones en un conjunto descendiente con exactamente k descensos [2].
Tipo III (p/q, p) Distribución Euleriana
El término distribución Euleriana también puede referirse a una distribución Tipo III (p/q, p) [3]. El artículo de Biometrika de Kendall de 1948, titulado «Sobre algunos modos de crecimiento de la población que conducen a la distribución de la serie logarítmica de RA Fisher», se refiere a los números relativos de animales de diferentes especies obtenidos al tomar muestras aleatorias de una población heterogénea. Fisher asumió que para una determinada especie, el número de individuos capturados en un tiempo específico se distribuiría como una variable de Poisson con expectativa ωt, donde ω es la “abundancia intrínseca”. La siguiente fórmula, que describe la distribución de ω, se menciona como una forma euleriana (o χ2): Donde
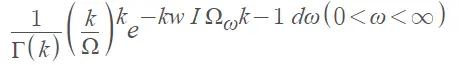
- Ω es el valor medio de ω.
- k es un parámetro constante.
Referencias
[1] Mansour, T. y Munagi, A. (2010). Enumeración de particiones por subidas, niveles y bajadas. En Patrones de Permutación. Prensa de la Universidad de Cambridge.[2] Hibi y Tsuchiya. (2019). Combinatoria algebraica y geométrica en politopos de celosía: actas del taller de verano sobre politopos de celosía. Científico Mundial.
[3] Kendall, DG (1948). Sobre algunos modos de crecimiento de la población que conducen a la distribución de series logarítmicas de RA Fisher . Biometrika, 35(1/2), 6–15. https://doi.org/10.2307/2332624

