Actualizado por ultima vez el 5 de enero de 2023, por Luis Benites.
Es posible que desee leer este artículo primero: ¿Qué es un logaritmo?
¿Qué es una distribución lognormal?
Una distribución lognormal (log-normal o Galton) es un tipo de distribución de probabilidad que se utiliza para describir variables que tienen valores que están distribuidos de manera asimétrica y que pueden tomar valores muy grandes.
La distribución lognormal se caracteriza por dos parámetros: el promedio y la desviación estándar de la variable original (no transformada). La distribución lognormal se obtiene al aplicar la transformación logarítmica a una distribución normal.
La distribución lognormal se utiliza a menudo para describir variables que crecen de manera exponencial, como el tamaño de las empresas o la concentración de una sustancia en un medio. También se utiliza en finanzas para modelar la distribución del rendimiento de los activos financieros.
Tambien se entiende una distribución lognormal (log-normal o Galton) como una distribución de probabilidad con un logaritmo distribuido normalmente. Una variable aleatoria se distribuye lognormalmente si su logaritmo se distribuye normalmente.
Las distribuciones sesgadas con valores medios bajos, gran varianza y valores totalmente positivos a menudo se ajustan a este tipo de distribución. Los valores deben ser positivos ya que log(x) existe solo para valores positivos de x.
La función de densidad de probabilidad se define por la media μ y la desviación estándar , σ:
La forma de la distribución lognormal está definida por tres parámetros:
- σ, el parámetro de forma . También la desviación estándar para el lognormal, esto afecta la forma general de la distribución. Por lo general, estos parámetros se conocen a partir de datos históricos. A veces, es posible que pueda estimarlo con datos actuales. El parámetro de forma no cambia la ubicación o la altura del gráfico; solo afecta la forma general.
- m, el parámetro de escala (también es la mediana). Este parámetro reduce o estira el gráfico.
- Θ (o μ), el parámetro de ubicación , que le indica dónde se encuentra el gráfico en el eje x.
La distribución lognormal estándar tiene un parámetro de ubicación de 0 y un parámetro de escala de 1 (que se muestra en azul en la imagen a continuación). Si Θ = 0, la distribución se denomina distribución lognormal de 2 parámetros.
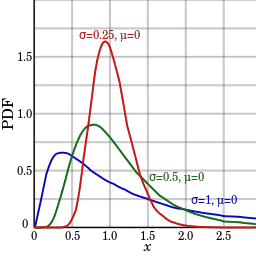
Algunos ejemplos de funciones de densidad lognormales. Imagen: Por Krishnavedala|Wikimedia Commons
¿Cuándo se utilizan las distribuciones lognormales?
La distribución más utilizada (y la más familiar) en ciencia es la distribución normal . La conocida “ curva de campana ” modela muchos fenómenos naturales, desde los más simples (pesos o alturas) hasta los más complejos. Por ejemplo, el siguiente fenómeno se puede modelar con una distribución lognormal:
- Producción de leche por vacas.
- Vidas de unidades industriales con modos de falla que se caracterizan por fatiga-esfuerzo.
- Cantidades de lluvia.
- Distribuciones de tamaño de las gotas de lluvia.
- El volumen de gas en una reserva de petróleo.
Se pueden modelar muchos más fenómenos con la distribución lognormal, como la duración de los períodos latentes de enfermedades infecciosas o la abundancia de especies 1 .
Otros nombres para el lognormal
Históricamente, la distribución lognormal ha recibido muchos nombres, entre ellos:
- La distribución de Galton o Galton (después del estadístico victoriano Francis Galton).
- Distribución de Galton-McAlister (McAlister fue otro estadístico victoriano que publicó una descripción de la distribución con Galton).
- Distribución de Gibrat , en honor al economista francés del siglo XX que demostró que los logaritmos de ciertas variables económicas (como la distribución de fábricas por número de trabajadores) seguían una distribución normal.
- Distribución Cobb-Douglas (después de los economistas del siglo XX Charles Cobb y Paul Douglas). Este término se usa exclusivamente en economía, donde se aplica a los datos de producción.
¡ Visite nuestro canal de YouTube para ver cientos de videos de ayuda sobre probabilidad y estadísticas!
Referencias:
Aitchison, J. y Brown, JAC La distribución lognormal, con especial referencia a su uso en economía . Nueva York: Cambridge University Press, 1957.
Balakrishnan, N. y Chen, WWS Handbook of Tables for Order Statistics from Lognormal Distributions with Applications. Ámsterdam, Países Bajos: Kluwer, 1999.
Crow, EL y Shimizu, K. (Ed.). Distribuciones Lognormales: Teoría y Aplicaciones. Nueva York: Dekker, 1988.
Limpert et al. Distribuciones logarítmicas normales en las ciencias: claves y pistas.
