Contenido de este artículo
Actualizado el 23 de abril de 2022, por Luis Benites.
La distribución multinomial se usa para encontrar probabilidades en experimentos donde hay más de dos resultados.
Experimentos binomiales vs. multinomiales
El primer tipo de experimento introducido en la estadística elemental suele ser el experimento binomial , que tiene las siguientes propiedades:
- Número fijo de n ensayos.
- Cada ensayo es un evento independiente .
- Solo dos resultados son posibles (Éxito y Fracaso).
- La probabilidad de éxito (p) de cada prueba es constante.
- Una variable aleatoria Y= el número de éxitos.
Un experimento multinomial es casi idéntico con una diferencia principal: un experimento binomial puede tener dos resultados, mientras que un experimento multinomial puede tener múltiples resultados.
Ejemplo : Lanzas un dado diez veces para ver qué número sacas. Hay 6 posibilidades (1, 2, 3, 4, 5, 6), así que este es un experimento multinomial. Si tiras el dado diez veces para ver cuántas veces sacas un tres, sería un experimento binomial (3 = éxito, 1, 2, 4, 5, 6 = fracaso).
Un experimento binomial tendrá una distribución binomial . Un experimento multinomial tendrá una distribución multinomial.
Ejemplo de distribución multinomial
Los jugadores de tres cartas juegan una serie de partidos. La probabilidad de que el jugador A gane cualquier juego es del 20 %, la probabilidad de que el jugador B gane es del 30 % y la probabilidad de que el jugador C gane es del 50 %. Si juegan 6 juegos, ¿cuál es la probabilidad de que el jugador A gane 1 juego, el jugador B gane 2 juegos y el jugador C gane 3?
Use la siguiente fórmula para calcular las probabilidades ( ¿Necesita ayuda? ¡Consulte nuestra página de tutoría! ): donde:
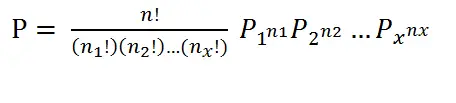
- n = número de eventos
- n 1 = número de resultados, evento 1
- n 2 = número de resultados, evento 2
- n 3 = número de resultados, evento x
- p 1 = probabilidad de que ocurra el evento 1
- p 2 = probabilidad de que ocurra el evento 2
- p x = probabilidad de que ocurra el evento x
Usando los datos de la pregunta, obtenemos:
- n = 12 (6 juegos en total).
- n 1 = 1 (el jugador A gana).
- n 2 = 2 (el jugador B gana).
- n 3 = 3 (el jugador C gana).
- p 1 = 0,20 (probabilidad de que gane el jugador A).
- p 2 = 0,30 (probabilidad de que gane el jugador B).
- p 3 = 0,50 (probabilidad de que gane el jugador C).
Poniendo esto en la fórmula, obtenemos:
![]()
¡ Visite nuestro canal de YouTube para ver cientos de videos de ayuda sobre estadísticas!
Referencias
Beyer, WH CRC Standard Mathematical Tables, 28.ª ed . Boca Ratón, Florida: CRC Press, pág. 532, 1987.
Papoulis, A. Probabilidad, variables aleatorias y procesos estocásticos, 2ª ed . Nueva York: McGraw-Hill, 1984.
