Actualizado por ultima vez el 13 de noviembre de 2021, por Luis Benites.
Los espacios muestrales introducidos en las primeras clases de probabilidad suelen ser discretos . Es decir, están formados por una cantidad finita (fija) de números. Por ejemplo, si lanza un dado, el espacio muestral (Ω) es [1, 2, 3, 4, 5, 6]. Tirar un dado de veinte caras o elegir una carta de un mazo produce espacios muestrales discretos. Un espacio muestral continuo se basa en los mismos principios, pero tiene un número infinito de elementos en el espacio. En otras palabras, no puede escribir el espacio de la misma manera que escribiría el espacio de muestra para una tirada de dado. Con un espacio de muestra continuo, aún estaría escribiendo números mucho después de que el sol haya implosionado en un agujero negro.
Ejemplo de espacio muestral continuo
La siguiente imagen muestra un espacio de muestra continuo: un área de 2 unidades de alto y 2 unidades de ancho. Imagina que el espacio representa un juego en el que se deja caer un dardo en el espacio y aterriza en un lugar aleatorio. ¿Cuáles son las probabilidades de que el dardo caiga en el lugar que se muestra en la imagen? Puede que le sorprenda saber que las probabilidades de que la pelota aterrice en cualquiera de esos dos puntos son cero. De hecho, las probabilidades de que el dardo caiga en cualquier
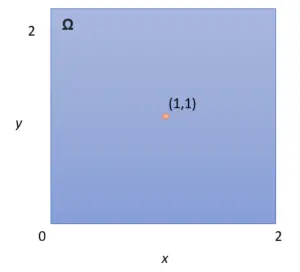spot en absoluto es igual a cero. Digamos que el dardo cae en (1, 1). También podría aterrizar un pelo a la derecha, en (1.001, 1). O, una fracción aún más pequeña a la derecha, en (1.0000000001, 1). Si tratas de anotar todos los lugares posibles en los que podría caer el dardo, no podrás hacerlo, porque hay un número infinito de espacios en los que podría caer la pelota. Si tiene un problema con esta lógica, no está solo. Es un ejemplo de cómo pensamos que funciona el mundo y cómo funciona realmente . Un ejemplo famoso de cómo el infinito interfiere con la lógica es la paradoja de Zeno (también conocida como “&helli[;la liebre nunca puede alcanzar a la tortuga en una carrera”).
Un enfoque más moderno es utilizar el problema en términos de límites . En términos simples, un límite es el número muy cercano al que estás midiendo. En el caso de todos estos ceros (1.001, 1.0000001, 1. 00000000000001, etc.), podría decir que todos están muy cerca de 1, lo que le da muchos menos puntos con los que lidiar. Para el problema anterior, podría obtener una probabilidad muy razonable si pudiera todas las coordenadas numeradas enteras posibles: (0, 1), (0, 2), (0, 3) y así sucesivamente.
Referencias
Bertsekas, D. y Tsitsiklis, J. (2008). Introducción a la probabilidad. Atenea Científica.
