Experimento Binomial Negativo / Distribución: Definición, Ejemplos

Actualizado el 26 de enero de 2022, por Luis Benites.

Imagen: UCSF

El experimento binomial negativo es casi lo mismo que un experimento binomial con una diferencia: un experimento binomial tiene un número fijo de intentos.

Si las siguientes cinco condiciones son verdaderas, el experimento es binomial :

1. Número fijo de n ensayos.
2. Cada ensayo es independiente .
3. Solo dos resultados son posibles (Éxito y Fracaso).
4. La probabilidad de éxito (p) de cada prueba es constante.
5. Una variable aleatoria Y= el número de éxitos.

Ejemplo : tome una baraja estándar de cartas, mézclelas y elija una carta. Vuelva a colocar la tarjeta y repita veinte veces. Y es el número de ases que sacas.

El binomio negativo es similar al binomio con dos diferencias (concretamente a los números 1 y 5 de la lista anterior):

• El número de intentos, n, no es fijo .
• Una variable aleatoria Y= el número de intentos necesarios para lograr r éxitos.

Ejemplo : tome una baraja estándar de cartas, mézclelas y elija una carta. Vuelve a colocar la carta y repite hasta que hayas sacado dos ases. Y es el número de sorteos necesarios para sacar dos ases. Como el número de intentos no es fijo (es decir, se detiene cuando saca el segundo as), esto lo convierte en una distribución binomial negativa.

¿Qué es una distribución binomial negativa?

Una distribución binomial negativa (también llamada Distribución Pascal) es una distribución de probabilidad discreta para variables aleatorias en un experimento binomial negativo.

La variable aleatoria es el número de intentos repetidos, X, que producen un cierto número de éxitos, r. En otras palabras, es el número de fracasos antes de un éxito. Esta es la principal diferencia con la distribución binomial : con una distribución binomial regular, estás viendo el número de éxitos. Con una distribución binomial negativa, lo que cuenta es el número de fallas.

¿Por qué se llama Binomial Negativo?

Cuando escuche el término negativo, podría pensar que una distribución positiva se invierte sobre el eje x, lo que la convierte en negativa. Sin embargo, la parte «negativa» de la binomial negativa en realidad proviene del hecho de que una faceta de la distribución binomial se invierte: en un experimento binomial , se cuenta el número de éxitos en una cantidad fija de intentos; en el ejemplo anterior, estás contando cuántos ases sacas. En un experimento binomial negativo, estás contando los fallos, o cuántas cartas te hacen falta para elegir dos ases.

La fórmula binomial negativa

Probabilidad :
b*(x; r, P) = _x-1 C _r-1 * P ^r * (1 – P) ^{x – r}
donde x=número de intentos
r = Éxitos

Media :
μ = r / P
donde r es el número de intentos
P = probabilidad de éxito para cualquier intento

Resolver problemas de experimentos binomiales negativos

La pmf para la distribución binomial negativa es: Donde: r es el número de éxitos yp = la probabilidad de éxito.

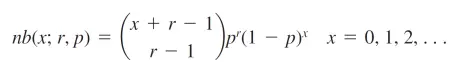
Ejemplo de pregunta: está encuestando a personas que salen de una cabina de votación y les pregunta si votaron de manera independiente. La probabilidad (p) de que una persona vote independiente es del 20%. ¿Cuál es la probabilidad de que se deba preguntar a 15 personas antes de encontrar a 5 personas que votaron por su independencia?

Paso 1: encuentre p, r y X.
Se nos da (en la pregunta) que p = 20% (.2) y r = 5. El número de fallas, X, es 15 – 5 = 10.

Paso 2: Inserte esos valores del Paso 1 en la fórmula:

Paso 3: Resuelve . La primera parte (14 sobre 4) es una combinación (usa nuestra calculadora de combinaciones para encontrar 14 elige 4).
1001*.2 ⁵ *.8 ¹⁰ = 0.034.

La probabilidad de que tenga que pedirle a 15 personas que obtengan 5 votos por independiente es .034, o 3.4%.

La distribución geométrica es un caso especial de la distribución binomial negativa.