Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 6 de abril de 2022, por Luis Benites.
¿Qué es el factor de corrección de población finita?
El factor de corrección de población finita (FPC) se usa cuando toma muestras sin reemplazo de más del 5 % de una población finita . Es necesario porque, en estas circunstancias, el teorema del límite central no se cumple y el error estándar de la estimación (p. ej., la media o la proporción) será demasiado grande. En términos básicos, el FPC captura la diferencia entre el muestreo con reemplazo y el muestreo sin reemplazo.
La mayoría de las encuestas de la vida real involucran poblaciones finitas muestreadas sin reemplazo. Por ejemplo, puede realizar una encuesta telefónica a 10.000 personas; una vez que se ha llamado a una persona, no se volverá a llamar.
Nota : una desventaja de usar el FPC es que puede causar incertidumbre al aplicar los resultados a una población más grande, por lo que debe tener cuidado al hacer inferencias.
Fórmula
La fórmula general es:
Donde:
- N = tamaño de la población ,
- n = tamaño de la muestra .
Si el valor calculado para el FPC es cercano a 1, puede ignorarse. A medida que el tamaño de la muestra cae por debajo del 5%, el valor se vuelve algo insignificante (un FPC es .998 para una muestra de 50).
La siguiente tabla de valores muestra cómo disminuye el FPC para una población de 10 000 a medida que aumenta el tamaño de la muestra:
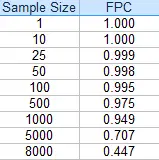
Cómo usar la fórmula
Básicamente, coloque la corrección al final de la fórmula que desea utilizar. Por ejemplo, el error estándar de la fórmula media es: Y con la corrección, la fórmula es:
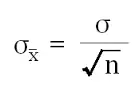
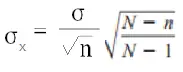
O, para un intervalo de confianza para una media y desviación estándar de población desconocida , la fórmula (con FPC) es: ![]()
Ejemplo
Se preguntó a treinta personas de una población de 300 cuánto tenían ahorrados. La media muestral (x̄) fue de $1500, con una desviación estándar muestral de $89,55. Construya una estimación del intervalo de confianza del 95% para la media de la población.
Solución (usando grados de libertad = n – 1 = 29) y t α/2 = 2,0452 para un nivel de confianza del 95 % ): = $1500 ± 33,44(0,9503) = $1500 ± 31,776 = $1468,22 ≤ μ ≤ $1531,78.
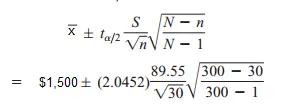
Referencias :
Kandethody, M. et al. Estadística Matemática con Aplicaciones . Elsevier India (2012). p.187.
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
