Actualizado por ultima vez el 12 de abril de 2022, por Luis Benites.
Es posible que desee leer estos artículos primero:
¿Qué es un intervalo de confianza?
¿Qué es una distribución binomial?
¿Qué es un intervalo de confianza binomial?
El intervalo de confianza binomial es una medida de incertidumbre para una proporción en una población estadística . Toma una proporción de una muestra y la ajusta por error de muestreo .
Supongamos que necesita un intervalo de confianza de 100(1-α) (donde α es el nivel de significación ) en un determinado parámetro p para una distribución binomial . Exactamente cómo lograría esto depende de los valores de n (su tamaño de muestra ) y p :
- Tamaño de muestra grande (> 15) y p grande (≥ 0,1): el método de aproximación normal funciona bien (Herson, 2009) a menos que la proporción sea cercana a 0 o 1 (Razdolsky, 2014). La regla general es que puede usar la aproximación normal cuando n * p y n * q (q es solo 1 – p) son mayores que 5. Para obtener más información, consulte: Uso de la aproximación normal para resolver una distribución binomial problema _
- Tamaño de muestra grande (> 15) y p pequeña (< 0,1): la aproximación de Poisson para el binomio es una mejor opción (Montgomery, 2001).
- Muestras pequeñas (15 o menos) : se debe usar una tabla binomial para encontrar el intervalo de confianza binomial para p.
Todas las fórmulas asociadas con un intervalo de confianza binomial funcionan bajo el supuesto de una distribución binomial subyacente. En otras palabras, su experimento tiene un número fijo de intentos con dos resultados, un «éxito» o un «fracaso». El éxito y el fracaso son términos genéricos para dos resultados opuestos, que pueden ser sí/no, negro/blanco, votó/no votó o una miríada de otras opciones.
1. N grande, P grande (aproximación normal)
Para muestras grandes, puede aproximar la binomial utilizando una distribución normal . Esto se justifica por el Teorema del Límite Central .
una muestra
La fórmula para el IC en el parámetro p es: El estimador puntual insesgado, p es la proporción de «éxitos» en un ensayo de Bernoulli . Como fórmula, eso es: Z alpha/2 es la puntuación z de un nivel alfa para una prueba de dos colas . Ver: ¿Qué es Z Alpha/2?
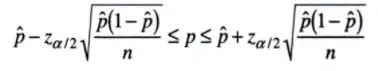
dos muestras
La fórmula para la diferencia en p 1 – p 2 es:
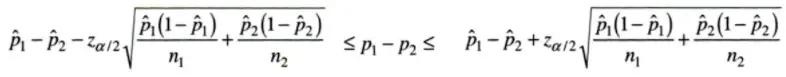
2. Aproximación usando la distribución de Poisson
Tienes un par de opciones aquí. La primera es usar una de las muchas calculadoras disponibles en línea. Una buena es esta , que le da valores para un IC del 95%. La segunda opción es utilizar una tabla, como la que se encuentra al final de este artículo: Tabla de intervalos de confianza exactos al 95% para la Distribución de Poisson.
Usemos un ejemplo para mostrar cómo funciona la tabla. Tiene una pequeña muestra de observaciones (n = 6) de una población total de 10,000. Para este bajo nivel de ocurrencia en la población, el Poisson da una buena aproximación al binomio. Para encontrar la media (μ) y el intervalo de confianza asociado:
- Localice los valores alto y bajo del 95 % en la tabla para los intervalos de confianza exactos del 95 % para la distribución de Poisson . . Para n = 6, el mínimo es 2,202 y el máximo es 13,06.
- Divide los números que encontraste en la tabla por el número de miembros de la población. En este ejemplo, hay 10 000 miembros, por lo que el intervalo de confianza es:
- 2,202 / 10.000 = 0,00022
- 13,06 / 10.000 = 0,001306
Tabla de IC del 95 % exacto para la distribución de Poisson
La siguiente tabla muestra los primeros valores para un límite de confianza exacto del 95 % para la distribución de Poisson (adaptado del Apéndice 1 de Bioestadística para ingenieros de Ahlbom):
| # Eventos observados | 95% bajo | 95% Alto |
| 0 | 0.000 | 3.689 |
| 1 | 0.025 | 5.572 |
| 2 | 0.242 | 7.225 |
| 3 | 0.619 | 8.767 |
| 4 | 1.090 | 10.24 |
| 5 | 1.623 | 11.67 |
| 6 | 2.202 | 13.06 |
| 7 | 2.814 | 14.42 |
| 8 | 3.454 | 15.76 |
| 7 | 2.814 | 14.42 |
| 8 | 3.454 | 15.76 |
| 9 | 4.115 | 17.09 |
| 10 | 4.795 | 18.39 |
| 11 | 5.491 | 19.68 |
| 12 | 6.201 | 20.96 |
| 13 | 6.922 | 22.23 |
| 14 | 7.654 | 23.49 |
| 15 | 8.395 | 24.74 |
| dieciséis | 9.145 | 25,98 |
| 17 | 9.903 | 27.22 |
| 18 | 10.67 | 28.45 |
| 19 | 11.44 | 29.67 |
| 20 | 12.22 | 30.89 |
Referencias
Herson, J. (2009). Comités de Monitoreo de Datos y Seguridad en Ensayos Clínicos . Prensa CRC.
Montgomery, D. (2001). Introducción al Control Estadístico de la Calidad. 4ª edición. Wiley & Sons.
Radolsky, L. (2014). Carga de fuego estructural basada en la probabilidad. Prensa de la Universidad de Cambridge.
