Contenido de este artículo
Actualizado el 28 de noviembre de 2021, por Luis Benites.
La divergencia de Kullback-Leibler (también llamada divergencia KL , ganancia de información de entropía relativa o divergencia de información ) es una forma de comparar las diferencias entre dos distribuciones de probabilidad p(x) y q(x). Más específicamente, la divergencia KL de q(x) de p(x) mide cuánta información se pierde cuando se usa q(x) para aproximar p(x). Responde a la pregunta: si utilicé la distribución «no del todo» correcta q(x) para aproximar p(x), ¿cuántos bits de información necesito para representar con mayor precisión p(x)?
Fórmula de divergencia KL
La fórmula para la divergencia de dos distribuciones de probabilidad discretas , definidas sobre una variable aleatoria x ∈ X, es la siguiente: Donde:
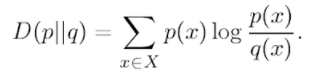
- X es el conjunto de todas las variables posibles para x.
La función logarítmica es nítida cercana a cero, por lo que esto puede permitir una detección sensible de pequeños cambios en la distribución de probabilidad (Sugiyama, 2015).
Para distribuciones de probabilidad continuas, la fórmula (Tyagi, 2018) implica cálculo integral :
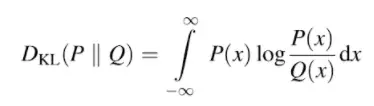
Distancia KL
La divergencia KL a veces se denomina distancia KL (o «modelo de distancia probabilística»), ya que representa una «distancia» entre dos distribuciones. Sin embargo, no es una métrica tradicional (es decir, no es una unidad de longitud). En primer lugar, no es simétrico en p y q; En otras palabras, la distancia de P a Q es diferente de la distancia de Q a P. Además, no satisface la desigualdad del triángulo (Manning & Schütze, 1999).
Referencias
Ganascia, J. et al. (2008). Discovery Science: 15th International Conference, DS 2012, Lyon, Francia, 29-31 de octubre de 2012, Actas. Saltador.
Han, J. (2008). Divergencia Kullback-Leibler. Recuperado el 16 de marzo de 2018 de: http://web.engr.illinois.edu/~hanj/cs412/bk3/KL-divergence.pdf
Kullback, S. & Liebler, R. (1951). Sobre Información y Suficiencia. Anales de Estadística Matemática. 22(1): 79-86.
Manning, C. y Schütze, H. (1999). Fundamentos del Procesamiento Estadístico del Lenguaje Natural. Prensa del MIT.
Sugiyama, M. (2015). Introducción al aprendizaje automático estadístico. Morgan Kaufman.
Tyagi, V. (2018). Recuperación de imágenes basada en contenido: ideas, influencias y tendencias actuales. Saltador.
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
