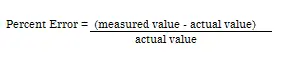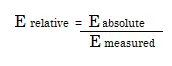Actualizado por ultima vez el 29 de noviembre de 2021, por Luis Benites.
¿Qué es el error de medición?
El error de medición (también llamado error de observación) es la diferencia entre una cantidad medida y su valor real. Incluye errores aleatorios (errores naturales que se esperan con cualquier experimento) y errores sistemáticos (causados por un instrumento mal calibrado que afecta todas las mediciones).
Por ejemplo, supongamos que está midiendo los pesos de 100 atletas de maratón. La báscula que utiliza tiene un error de una libra: este es un error sistemático que dará como resultado que todos los cálculos del peso corporal de los atletas tengan un error de una libra. Por otro lado, digamos que su escala fue precisa. Algunos atletas pueden estar más deshidratados que otros. Algunos pueden tener ropa más mojada (y por lo tanto más pesada) o una botella de 2 oz. barra de chocolate en un bolsillo. Estos son errores aleatorios y son de esperar. De hecho, todas las muestras recolectadas tendrán errores aleatorios; en su mayor parte, son inevitables.
Los errores de medición pueden aumentar rápidamente de tamaño cuando se usan en fórmulas. Por ejemplo, si está utilizando un pequeño error en una medición de velocidad para calcular la energía cinética, sus errores pueden cuadriplicarse fácilmente. Para dar cuenta de esto, debe usar una fórmula para la propagación de errores cada vez que use medidas inciertas en un experimento para calcular algo más.
Diferentes medidas de error
Las diferentes medidas de error incluyen:
- Error absoluto: la cantidad de error en su medición. Por ejemplo, si se sube a una báscula y dice 150 libras pero sabe que su peso real es 145 libras, entonces la báscula tiene un error absoluto de 150 libras – 145 libras = 5 libras.
- Mayor error posible : definido como la mitad de la unidad de medida. Por ejemplo, si usa una regla que mide en yardas enteras (es decir, sin fracciones), entonces el mayor error posible es media yarda.
- Error del instrumento: error causado por un instrumento inexacto (como una escala que está mal o un cuestionario mal redactado).
- Margen de error : una cantidad por encima y por debajo de su medida. Por ejemplo, podría decir que el bebé promedio pesa 8 libras con un margen de error de 2 libras (± 2 libras).
- Error de ubicación de medición : causado por un instrumento colocado en un lugar donde no debería, como un termómetro dejado a pleno sol.
- Error del operador : factores humanos que causan errores, como leer una escala incorrectamente.
- Porcentaje de error : otra forma de expresar el error de medición. Definido como:
- Error relativo : la relación entre el error absoluto y la medida aceptada. Como fórmula, eso es:
Formas de reducir el error de medición
- Vuelva a verificar todas las medidas para verificar su precisión . Por ejemplo, ingrese dos veces todas las entradas en dos hojas de trabajo y compárelas.
- Vuelva a verificar que sus fórmulas sean correctas.
- Asegúrese de que los observadores y los tomadores de medidas estén bien capacitados.
- Realice la medición con el instrumento que tenga la mayor precisión.
- Tome las medidas bajo condiciones controladas.
- Prueba piloto de sus instrumentos de medición. Por ejemplo, organice un grupo focal y pregunte cuán fáciles o difíciles fueron de entender las preguntas.
- Use múltiples medidas para la misma construcción. Por ejemplo, si está evaluando la depresión, use dos cuestionarios diferentes.
Procedimientos estadísticos para evaluar el error de medición
Los siguientes métodos evalúan la “confiabilidad absoluta”:
- Error estándar de medición (SEM) : estima cómo las mediciones repetidas tomadas en el mismo instrumento se estiman alrededor de la puntuación real.
- Coeficiente de variación (CV) : una medida de la variabilidad de una distribución de puntuaciones o mediciones repetidas. Los valores más pequeños indican una variación más pequeña y, por lo tanto, valores más cercanos a la puntuación real.
- Límites de concordancia (LOA) : da una estimación del intervalo en el que se encuentra una proporción de las diferencias entre las mediciones.
Referencias
Beyer, WH CRC Standard Mathematical Tables, 31ª ed. Boca Raton, FL: CRC Press, págs. 536 y 571, 2002.
Dodge, Y. (2008). La Enciclopedia Concisa de Estadística . Saltador.
Vogt, WP (2005). Diccionario de estadística y metodología: una guía no técnica para las ciencias sociales . SABIO.
Wheelan, C. (2014). Estadísticas desnudas . WW Norton y compañía
