Contenido de este artículo
Actualizado el 13 de octubre de 2021, por Luis Benites.
Kriging es un tipo de regresión que proporciona una estimación de datos por mínimos cuadrados (Remy et. al, 2011). Utiliza puntuaciones z para generar un modelo de superficie estimado a partir de la descripción espacial de un conjunto disperso de puntos de datos. Se originó en la geología minera y ahora es una parte importante de la caja de herramientas de geoestadística. También tiene aplicaciones en ingeniería informática, teledetección y ciencias ambientales.
Un punto fuerte de este tipo de interpolación es que no solo genera un modelo espacial interpolado, también genera una estimación de la incertidumbre de cada punto en ese modelo.
A diferencia de la regresión lineal o la interpolación ponderada de distancia inversa, la interpolación de kriging se basa principalmente en observaciones empíricas, los puntos de datos de muestra observados, en lugar de en un modelo asumido previamente.
La interpolación da más peso a los puntos de muestra cercanos a una ubicación que a los que están más lejos y, para reducir el sesgo de muestreo , le da menos peso a los conglomerados que a los puntos únicos. El valor de cada punto se calcula de tal manera que se minimice el error esperado para ese punto en particular.
Ejemplo
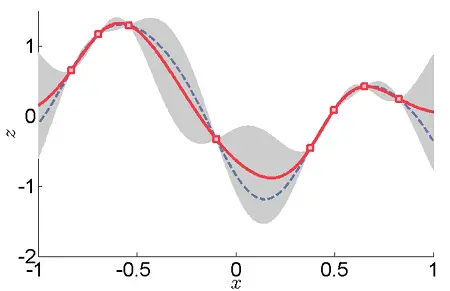 El gráfico anterior es un ejemplo de interpolación de datos unidimensionales mediante kriging.
El gráfico anterior es un ejemplo de interpolación de datos unidimensionales mediante kriging.
- Las áreas grises son los intervalos de confianza normalmente distribuidos .
- La línea roja representa la interpolación de kriging, que corre a lo largo de las medias de los intervalos de confianza normalmente distribuidos.
- Los cuadrados muestran los puntos de datos originales.
- La curva discontinua muestra una spline suave. Sin embargo, esto se aleja significativamente de los valores intermedios esperados dados por los medios.
Limitaciones de la interpolación de Kriging
Kriging asume que el espacio que se estudia es estacionario ; es decir, que la distribución de probabilidad conjunta no cambie a lo largo del espacio de estudio.
También asume una propiedad llamada isotropía ; que hay uniformidad en todas direcciones.
Si estas condiciones son difíciles de cumplir, el método se vuelve problemático. Sin embargo, en el kriging universal , el requisito estacionario se relaja.
La precisión de su modelo será limitada si los datos no están espacialmente correlacionados , si su distribución es limitada o si la cantidad de puntos de datos es pequeña.
Referencias
- Documentación de ArcMap. Recuperado de http://desktop.arcgis.com/en/arcmap/10.3/tools/3d-analyst-toolbox/how-kriging-works.htm el 24 de junio de 2018
- Clark, I. ¿Qué es Kri-ging de todos modos? Recuperado de http://www.kriging.com/whatiskri-ging.html el 24 de junio de 2018
- Geografía SIG. La predicción es fuerte en este. (Cómo interpolar con geoestadística) Recuperado de https://gisgeography.com/kriging-interpolation-prediction/ el 24 de junio de 2018
- Método de Salud de la Población. Recuperado de
https://www.mailman.columbia.edu/research/population-health-methods/kri-ging el 24 de junio de 2018. - Remy et. al (2011) Geoestadística aplicada con SGeMS: Guía del usuario . Prensa de la Universidad de Cambridge.
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
