Actualizado por ultima vez el 3 de mayo de 2022, por Luis Benites.
¿Qué es la Ley de los Grandes Números?
La Ley de los Grandes Números nos muestra que si tomas un experimento impredecible y lo repites suficientes veces, lo que obtendrás será un promedio .
Supongamos que tuvo un experimento en el que estaba lanzando una moneda justa con probabilidad p (para una moneda justa, p = 0,5). Por unos pocos lanzamientos de moneda, es posible que no se acerque a p = 0.5. Sin embargo, a medida que realiza más y más experimentos, su proporción experimental de resultados con probabilidad p̂ n convergerá a p .
En términos simples: si repitió un experimento muchas, muchas, muchas veces… comenzará a ver un patrón esperado, lo que hará que sea más fácil calcular las probabilidades.
Un ejemplo sencillo: tira un dado y obtendrás un número aleatorio (para un dado de seis caras, obtendrás 1,2,3,4,5,6). Lanza el dado 100.000 veces y obtendrás un promedio de 3,5, que es el valor esperado .
Ley de los grandes números frente al teorema del límite central
Ambas leyes nos dicen que dada una cantidad suficientemente grande de puntos de datos, esos puntos de datos darán como resultado comportamientos predecibles. El teorema del límite central muestra que a medida que el tamaño de una muestra tiende a infinito , la forma de la distribución de la muestra se aproximará a la distribución normal ; la Ley de los Grandes Números le muestra dónde es probable que se encuentre el centro de esa curva normal.
Ley fuerte y débil de los grandes números
La Ley de los Grandes Números a veces se llama la Ley Débil de los Grandes Números para distinguirla de la Ley Fuerte de los Grandes Números . Las dos versiones de la ley son diferentes según el modo de convergencia . Como sugiere su nombre, la ley débil es más débil que la ley fuerte. Básicamente, la ley débil es donde la media de la muestra converge a la media esperada en el cuadrado medio y en la probabilidad; la ley fuerte de los grandes números es donde la media muestral M n converge a la media esperada μ con probabilidad 1.
La ley fuerte implica la ley débil, pero considera una secuencia infinita de resultados. Por lo tanto, la ley débil suele ser mejor para aplicaciones prácticas.
La ley fuerte de los números se puede definir con mayor precisión con algunos términos del cálculo :
Dada una secuencia infinita de observaciones: Donde:
- ℙ = probabilidad de un evento,
- p ̂ = proporción experimental,
- p = proporción esperada,
- lím = límite .
Esto es afirmar que, con una probabilidad de 1, el límite
de la sucesión p ̂ será igual a p .
La ley débil de los grandes números establece que cuando n → ∞, la probabilidad de que la desigualdad | p ̂ n – p | ≥ ε tiende a cero, independientemente de cuán pequeño sea ε. En notación, eso es: (Donde épsilon (ε) es un número pequeño, cercano a cero).
La siguiente prueba usa la definición epsilon-delta de un límite para mostrar que el LLN fuerte implica el LLN débil (Kjos-Hanssen, 2019):
Sea ε > 0 dado. Como tenemos: ℙ(existe un m tal que para todo n ≥ m, |p̂ n – p| < ε) = 1. Podemos concluir que, para cada δ > 0, existe un m tal que ℙ(para todo n ≥ m, |p̂ n – p| < ε) ≥ 1 – δ. En particular, para todo n ≥ m, ℙ(|p̂ n – p| < ε) ≥ 1 – δ.
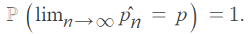
ley de los promedios
La ley de los promedios a veces se cuela en los libros de texto en lugar de la Ley de los Grandes Números. Los dos términos no son, técnicamente, intercambiables.
- La Ley de los Números Grandes: Si toma un experimento impredecible y lo repite suficientes veces (es decir, para un número muy grande), lo que obtendrá será un promedio.
- La Ley de los Promedios: la creencia de que la Ley de los Números Grandes también se aplica a los números pequeños.
Son básicamente lo mismo, excepto que la ley de los promedios extiende la ley de los números grandes para aplicarla también a los números pequeños. La ley de los grandes números es un concepto estadístico que siempre funciona; la ley de los promedios es un término común que a veces funciona… ya veces no.
La ley de los promedios y por qué no funciona
Un concepto erróneo común es que los números de lotería que no han aparecido en un tiempo saldrán a la luz. No lo son; cualquier número tiene la misma probabilidad de salir que el siguiente. Piénsalo: si hubiera algún patrón detrás de los números de la lotería (no lo hay), todos los matemáticos seríamos ricos. Y la mayoría de nosotros todavía estamos arruinados.
Un ejemplo famoso de la ley de los promedios en los juegos de azar se llama la falacia del jugador (ver más abajo), que consiste en creer que una racha perdedora se “igualará” al final . no lo hará Por ejemplo, supongamos que está apostando al rojo en una mesa de ruleta, pero pierde diez veces seguidas y todas las bolas caen en el negro. Piensas que la ley de los promedios dará como resultado una racha de rojos. No lo hará. La probabilidad de obtener un rojo en cualquier giro es 1/2, sin importar cuántas veces se gire. Una racha perdedora es solo eso: una racha perdedora. Es tan probable que el próximo giro sea negro como rojo.
La razón por la que los rojos y los negros no se equilibran es porque tienes una pequeña cantidad de giros. Podría permanecer al volante durante un par de horas y apostar 200 veces, pero sigue siendo un número relativamente pequeño (en comparación con un millón o un billón) y la ley de los promedios no dice nada acerca de los números pequeños. Si permaneció al volante durante una cantidad infinita de giros (en la práctica, un par de millones deberían bastar), eventualmente los giros se igualarán a 50% negro y 50% rojo.
Si aún no estás convencido, prueba esta calculadora de lanzamiento de dados de Wolfram . Puede establecer el número de rollos como una pequeña cantidad (por ejemplo, hasta 50) y verá algunos resultados bastante aleatorios. Aumente el número de rollos a unos pocos miles y verá que los resultados comienzan a converger en un promedio .
¿Qué es la falacia del jugador?
La falacia del jugador es la creencia errónea de que si tienes una racha de suerte, las probabilidades son que a la larga tus posibilidades se equilibren. También funciona a la inversa con una racha de mala suerte. Un ejemplo simple: lanzas una moneda 10 veces, con la esperanza de obtener cara. La lógica te dice que si lanzas la moneda 10 veces, 5 lanzamientos resultarán en cruz y 5 en cara. Los primeros cinco lanzamientos de moneda son cara. Usted (erróneamente) piensa que los próximos cinco lanzamientos probablemente serán cinco cruces.
P. Lanzas una moneda justa 10 veces seguidas y obtienes 10 caras. Si continúas lanzando la moneda hasta que la hayas lanzado cien veces, ¿se igualarán las caras y las cruces para que termines con aproximadamente 50 cruces y 50 caras?
Si respondiste que sí , entonces acabas de caer en la falacia del jugador. Si lanzas una moneda 10 veces y obtienes todas caras, ese bistec poco común no será igualado por una racha de cruces en el futuro.
Una falacia es una creencia errónea, generalmente una creencia basada en un argumento erróneo. El razonamiento (o argumento) para responder “sí” a la pregunta anterior es que dada una moneda justa, si la lanzas suficientes veces, obtendrás un 50 por ciento de cara y un 50 por ciento de cruz.* Y, por lo general, al lanzarla cien veces es suficiente para igualar las caras y las cruces. Sin embargo, una racha de caras (o cruces) es muy inusual. De hecho, tienes la pequeña probabilidad del 00,098% de que eso suceda. Ahora considere lo que sucede en el decimotercer lanzamiento de la moneda: tiene un 50 por ciento de posibilidades de que salga cara o cruz. Y así para el lanzamiento 14 y el lanzamiento 15. Así que es probable que termines con (para los siguientes 90 lanzamientos) 45 caras y 45 cruces, lo que te da un total de 55 caras y 45 cruces.
Un segundo ejemplo de la falacia del jugador; juegas un juego en línea con uno de tus amigos y durante el último año has ganado el 50% de tus juegos. Tu amigo tiene una racha ganadora de 4 juegos seguidos. Piensas erróneamente que los próximos 4 juegos probablemente serán victorias para ti, ya que estás «a punto» de ganar.
La falacia del jugador inverso
La inversión de la falacia del jugador también es una falacia, donde (debido a que el jugador piensa que está en una «racha de suerte») es más probable que obtenga el mismo resultado (en el primer ejemplo anterior, más cruces).
La falacia del jugador también se conoce como la falacia de Montecarlo o la falacia de la madurez de las posibilidades .
Una broma (nuevamente contada en el sitio de Penn State ) cuenta la historia del hombre que no pudo abordar un avión cuando se descubrió que llevaba una bomba. Cuando se le pregunta por qué llevaba una bomba, razona: “Las posibilidades de que un avión tenga una bomba encima son muy pequeñas, ¡y ciertamente las posibilidades de tener dos son casi nulas!”. Del mismo modo, el héroe de El mundo según Garp compra una casa en la que acaba de estrellarse un avión. Su razonamiento es que las posibilidades de que otro avión se estrelle contra él son prácticamente nulas.
O qué tal sostener un pararrayos en una tormenta. Las posibilidades de que te caiga un rayo son bastante altas. Si te golpean una vez (y sobrevives), ¿vas a seguir sujetando el pararrayos? Probablemente no&diablos
*Técnicamente hablando, siempre que los resultados sean eventos independientes , la probabilidad es exactamente del 50 por ciento.
Referencias
Kjos-Hanssen, B. (2019). Estadísticas para estudiantes de cálculo. Recuperado el 28 de abril de 2021 de: https://dspace.lib.hawaii.edu/bitstream/10790/4572/s4cs.pdf
