Actualizado por ultima vez el 1 de diciembre de 2021, por Luis Benites.
¿Qué es la Media Cuadrática / Raíz Cuadrada Media?
La media cuadrática (también llamada raíz cuadrada media *) es un tipo de promedio. Mide la magnitud absoluta de un conjunto de números y se calcula mediante:
- Elevando al cuadrado cada número,
- Encontrar la media de estos cuadrados,
- Tomando la raíz cuadrada de ese promedio .
Si etiqueta cada elemento de su conjunto como x i , donde i es un número de índice que va del 1 al n, el RMS puede describirse como: RMS otorga mayor peso a los elementos más grandes de un conjunto y siempre es igual o mayor que la media aritmética “regular” (promedio).
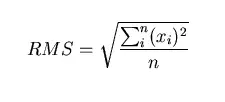
A veces, se dice que la media cuadrática es “igual que” la desviación estándar . Esto no es estrictamente cierto: la desviación estándar es en realidad igual a las desviaciones cuadráticas de la media del conjunto de datos. Por ejemplo, la media cuadrática se usa en las ciencias físicas como sinónimo de desviación estándar cuando se hace referencia a la «raíz cuadrada de la desviación cuadrática media de una señal desde una línea de base o ajuste dado» (Wolfram).
La media cuadrática también se llama raíz cuadrada media porque es la raíz cuadrada de la media de los cuadrados de los números en el conjunto.
* Nota : Esto es diferente del error cuadrático medio (RMSE) , que es un valor que se usa en el análisis de regresión para describir qué tan dispersos están los datos alrededor de una línea de regresión.
Fórmula
La media cuadrática es igual a la raíz cuadrada de la media de los valores al cuadrado. La fórmula es: Una fórmula equivalente tiene un signo de sumatoria ( sumación significa «sumar», por lo que aquí le está diciendo que sume todos los valores de x al cuadrado):
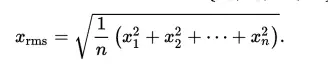
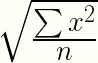
Ejemplos de la Raíz Cuadrada Media (RMS)
Para encontrar la raíz cuadrada media del conjunto {1, 3, 4}:
- Cuadre cada uno de los números
- Encuentre la media del Paso 1
- Encuentra la raíz cuadrada del paso 2
Ejemplo resuelto
Encuentra la raíz cuadrada media de 2, 4, 9, 10 y 12.
Paso 1: cuenta el número de artículos.
N = 5.
Deja este número a un lado por un momento.
Paso 2: Cuadre todos los números. 2 2 ,4 2 ,9 2 ,10 2 , 12 2 = 4, 16, 81, 100, 144.
Paso 3: Sume los números del Paso 2 hacia arriba: 4 + 16 + 81 + 100 + 144 = 345.
Paso 4: Divida el Paso 3 (la suma) por el Paso 1 (número de artículos en el conjunto):
345/5 = 69.
Paso 5: Encuentra la raíz cuadrada del Paso 4. √(69) = 8.31.
¡Eso es todo!
El RMS de cualquier serie de números idénticos positivos será ese mismo número, así como el promedio de una serie de números idénticos es el número mismo. El RMS de una serie de números idénticos negativos será el valor absoluto de ese número. Para valores positivos, el RMS es igual o un poco mayor que el promedio.
Aplicaciones de RMS
RMS es importante en muchas ramas de la física, la química y la ingeniería, y es un componente de las estadísticas matemáticas. Se puede utilizar para medir el ajuste de un estimador a un conjunto de datos.
Los cálculos RMS juegan un papel especialmente importante en la ingeniería eléctrica. Para una forma de onda de CA periódica y arbitraria, el voltaje RMS viene dado por:

La raíz cuadrática media también se utiliza para fines muy especializados, como la expresión del diámetro medio de los rodales en la silvicultura . En este caso, la media cuadrática del diámetro del rodal está más cerca de la media «verdadera» de una muestra de árboles que de la media aritmética.
RMS también se usa en cualquier lugar donde lo que importa es el cuadrado de los valores, en lugar de los valores mismos. Por ejemplo, la corriente eléctrica al cuadrado es proporcional a la potencia, por lo que si está interesado en la potencia total (en lugar de la corriente), este tipo de promedio es una buena opción.
Referencias
Gonick, L. (1993). La guía de dibujos animados para estadísticas Libro en rústica – Ilustrado . Harper Perennial.
Holmes, Susana. RMS. Notas del curso S60. Recuperado de http://statweb.stanford.edu/~susan/courses/s60/split/node49.html el 20 de noviembre de 2018.
Kenney, JF y Keeping, ES “Root Mean Square”. §4.15 en Matemáticas de Estadística, Pt. 1, 3ª ed. Princeton, NJ: Van Nostrand, págs. 59-60, 1962.
Wolfram. Media cuadrática. Disponible en: http://mathworld.wolfram.com/Root-Mean-Square.html

