Actualizado por ultima vez el 4 de marzo de 2022, por Luis Benites.
¿Qué es la media generalizada?
La media generalizada (también conocida como media de potencia o media de Hölder) es solo una forma de expresar la mayoría de las medias comunes (como la media aritmética ) en una fórmula: Si cambias λ (lo verás como p en algunas formas de la ecuación) a un valor particular, obtendrá la fórmula para uno de los medios comunes:
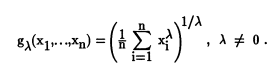
- -1 : media armónica,
- 1: media aritmética .
- 2: media cuadrática.
Sin embargo, son posibles otros medios reales e hipotéticos; de hecho, λ puede ser cualquier número distinto de cero de -∞ a ∞. Para valores muy cercanos a cero (estamos hablando de un límite de cálculo aquí), la función se aproxima a la media geométrica. Hipotéticamente, si pudieras poner 0 para λ, la ecuación sería la media geométrica exacta, pero como X 0 = 1, una potencia cero no funcionaría para esta fórmula.
Entrando en cosas más técnicas, la media generalizada se puede derivar de un par de maneras diferentes:
- Uso de estimaciones de mínimos cuadrados a partir de datos transformados.
- A partir de estimaciones de máxima verosimilitud .
Media generalizada ponderada / Media de potencia
Una media ponderada en matemáticas es cuando multiplicas tus puntajes separados por un factor de ponderación . Por ejemplo, su examen final que vale 100 puntos podría tener un factor de ponderación de 0,4 y las pruebas individuales podrían tener un factor de ponderación de 0,1 (consulte ¿Qué es una media ponderada? para ver un ejemplo paso a paso). El gen ponderado. mean funciona exactamente de la misma manera. La única diferencia entre esta fórmula y la fórmula que se muestra en la primera parte de este artículo es la adición de w i , un factor de ponderación.
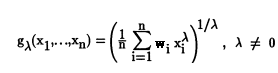
La fórmula media ponderada de la potencia/media generalizada.
Tenga en cuenta que la media generalizada no es lo mismo que la media generalizada de Kolmogorov, también llamada media cuasi aritmética o media f generalizada. Aunque son similares en concepto (es decir, ambos son formas de adaptar una fórmula a una variedad de medios), utilizan fórmulas diferentes para lograrlo.
Referencias:
Bullen, PS “The Power Means”. cap. 3 en Manual de medias y sus desigualdades . Dordrecht, Países Bajos: Kluwer, 2003.

