Actualizado por ultima vez el 6 de noviembre de 2021, por Luis Benites.
Problema del tanque alemán
El problema de los tanques alemanes es una forma de estimar el tamaño total de la población a partir de una pequeña muestra. Se usa comúnmente en estadísticas AP para enseñar sobre estimadores. El problema fue desarrollado originalmente por los Aliados durante la Segunda Guerra Mundial, cuando se utilizó para estimar el número total de tanques alemanes a partir de una pequeña cantidad de números de serie de tanques capturados, destruidos u observados. Se amplió para estimar el número de fábricas y otras piezas fabricadas. Hoy en día, la fórmula se ha aplicado para aplicaciones de amplio alcance, como estimar la cantidad de iPhones vendidos.
La idea es que los tanques fueran numerados 1,2,…x, donde “x” era el número total desconocido de tanques. Si conocemos solo algunos números de tanques, podemos usarlos para estimar x.
Fórmula
La fórmula para resolver el problema de los tanques alemanes es: Donde :
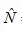= población máxima, - m = muestra máxima (es decir, el número de serie más alto),
- n = tamaño de la muestra .
Ejemplo
Problema de ejemplo: captura 5 tanques enemigos con los números de serie 1, 31, 43, 79 y 115. ¿Cuál es la población máxima probable?
Solución :
Paso 1: Inserte los valores dados en la fórmula. Para este ejemplo, el tamaño de la muestra es 5 y el valor más alto de la muestra es 115, entonces:
= 115 + (115 / 5) – 1
Paso 2: Resuelva:
= 115 + (115 / 5) – 1
= 115 + 23 – 1
= 138 – 1
= 137
La población máxima es 137.
La historia detrás del problema
En la Segunda Guerra Mundial, los Aliados no sabían cuántos tanques estaban fabricando los alemanes. Después de que se capturara un conjunto de tanques alemanes Mark V y los estadísticos teorizaron (correctamente) que los alemanes numeraron esos tanques secuencialmente a medida que salían de la línea de producción. Los estadísticos utilizaron la fórmula anterior para estimar que se fabricaban 246 tanques por mes entre junio de 1940 y septiembre de 1942; Esta fue una reducción significativa de las estimaciones de inteligencia que sitúan el número en alrededor de 1400. Después de la guerra, los aliados inspeccionaron los registros de producción de los alemanes y descubrieron que el número real de tanques producidos por mes era de 245, muy cerca de la estimación de los estadísticos.
Estimador imparcial de varianza mínima
La solución al problema del tanque es un ejemplo de un estimador imparcial de varianza mínima (MVUE) . Un estimador imparcial es una estadística precisa que se utiliza para aproximar un parámetro de población ; “Varianza mínima” significa que de todas las estimaciones posibles, la fórmula: es la que tiene la varianza más baja . Las «estimaciones posibles» incluyen todas las formas que se te ocurran que podrían estimar el número total de tanques. Además de la fórmula anterior, sus estimaciones podrían incluir:
- Duplicación de la media muestral .
- Multiplicando la desviación estándar de la muestra por cinco.
- Calcular el máximo muestral más el mínimo muestral.
Y así. El MVUE será la fórmula con la varianza más baja. En otras palabras, la fórmula m + (m/n) + 1 da un resultado más cercano a la media que cualquiera de las otras posibles fórmulas.
Referencias :
Davies, G. 2006. Gavyn Davies hace las matemáticas; Cómo una fórmula estadística ganó la guerra. El guardián. 19 de julio de 2006. Consultado el 14 de noviembre de 2016. Disponible en línea aquí .
