Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 21 de julio de 2024, por Luis Benites.
Puede que le resulte útil leer este artículo primero: ¿Qué es la heterocedasticidad?
¿Qué es la prueba de Breusch-Pagan-Godfrey?
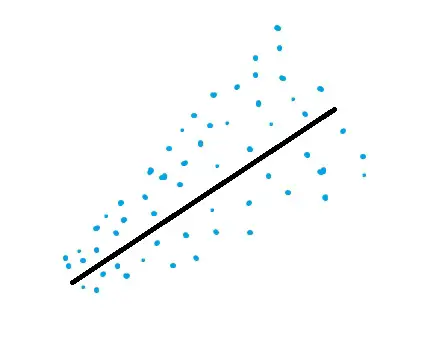
Datos heteroscedásticos.
La prueba de Breusch-Pagan-Godfrey (a veces abreviada como prueba de Breusch-Pagan) es una prueba de heteroscedasticidad de errores en la regresión. Heterocedasticidad significa “diferentemente disperso”; esto es opuesto a homocedástico, que significa “misma dispersión”. La homocedasticidad en la regresión es una suposición importante; si se viola la suposición, no podrá utilizar el análisis de regresión.
Ejecución de la prueba
El estadístico de prueba para la prueba de Breusch-Pagan-Godfrey es:
N * R 2 (con k grados de libertad )
Donde:
- n = tamaño de la muestra
- R 2 = R 2 ( Coeficiente de Determinación ) de la regresión de residuos al cuadrado de la regresión original.
- k = número de variables independientes .
La estadística de prueba sigue aproximadamente una distribución de chi-cuadrado .
- La hipótesis nula de esta prueba es que las varianzas del error son todas iguales.
- La hipótesis alternativa es que las varianzas del error no son iguales. Más específicamente, a medida que Y aumenta, las varianzas aumentan (o disminuyen).
Un valor chi-cuadrado pequeño (junto con un valor p pequeño asociado ) indica que la hipótesis nula es verdadera (es decir, que las varianzas son todas iguales).
Tenga en cuenta que la prueba de Breush-Pagan mide cómo aumentan los errores en la variable explicativa , Y. La prueba supone que las varianzas de error se deben a una función lineal de una o más variables explicativas en el modelo. Eso significa que la heteroscedasticidad aún podría estar presente en su modelo de regresión, pero esos errores (si están presentes) no están correlacionados con los valores de Y.
Si sospecha que un pequeño subconjunto de valores está causando heteroscedasticidad, puede ejecutar una prueba de Breusch-Pagan modificada solo en esos valores.
Precaución : algunos autores (incluidos Bickel (1978) y Koenker (1981)) han sugerido que la prueba estadística de Breusch-Pagan-Godfrey puede no ser precisa para datos no normales.
Referencias :
Bickel, PJ, 1978, Uso robusto de residuos I: Prueba de heteroscedasticidad y no linealidad, Annals of Statistics 6, 266-291.
Breusch, TS and AR Pagan, 1979, A simple test for heteroscedasticity and random coeficiency variation, Econometrica 47, 1287-1294.
Koenker, R., 1981, A note on studentizing a test for heteroscedasticity, Journal of Econometrics 17, 107-1 12
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
