Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 18 de mayo de 2022, por Luis Benites.
Mire el video para ver un ejemplo del MRT de Duncan, o siga leyendo a continuación.
Prueba de rango múltiple de Duncan DMRT 
Mira este video en YouTube .
¿No puedes ver el vídeo? Haga clic aquí
¿Qué es el MRT de Duncan?
Cuando ejecuta el Análisis de varianza (ANOVA) , los resultados le dirán si hay una diferencia en las medias . Sin embargo, no señalará qué medios son diferentes. La prueba de rango múltiple de Duncan (DMRT) es una prueba post hoc para medir diferencias específicas entre pares de medias.
La prueba de rango múltiple de Duncan fue diseñada originalmente por David B. Duncan como una alternativa de mayor potencia a Newman-Keuls . DMRT es más útil que LSD cuando se comparan pares de medias más grandes , especialmente cuando esos valores están en una tabla. DMRT tiende a requerir mayores diferencias entre las medias en comparación con el LSD, que protege contra el error de tipo I. Por ejemplo, mientras que el LSD podría decir que una diferencia de medias de 6 es significativa, el valor de DMRT podría ser el doble, previniendo la posibilidad de marcar diferencias significativas cuando no lo son.
La tecnología generalmente se usa para encontrar valores para DMRT. A mano, el procedimiento es esencialmente el mismo que para el LSD de Fisher . La principal diferencia es que en lugar de buscar el valor crítico en una tabla t, buscaría en una tabla q.
Ejemplo de prueba de rango múltiple de Duncan
Tenga en cuenta que esta prueba asume que ha ejecutado ANOVA y tiene un resultado significativo .
Calcule DMRT para la siguiente salida:
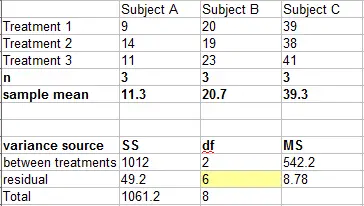
Paso 1: Clasifique los tratamientos de la media más alta a la más baja . Para este conjunto de datos, las medias en orden son:
- 39.3
- 20.7
- 11.3
Los siguientes pasos son comparar la media más alta (39,3) con la media más baja (11,3), que tienen una diferencia de 39,3 – 11,3 = 28.
Paso 2: busque el valor de q en esta tabla . Con 3 tratamientos y 6 grados de libertad para el término de error , el valor de Q es 4,34.
Paso 3: Encuentra σd 2 .
σd 2 = 2 x cuadrado medio residual / n = (2 * 8,78) /3 = 5,85
Paso 4: Saque la raíz cuadrada del Paso 3:
σd = √5.85 = 2.42.
Paso 5: Multiplique σd (Paso 4) por el valor q (Paso 2):
2,42 * 4,34 = 10,5.
La diferencia entre la media más alta y la más baja es superior a 10,5, por lo que la media más alta es significativamente diferente de la media más baja.
Los siguientes pasos son comparar la segunda media más alta (20,7) con la media más baja (11,3), que tienen una diferencia de 20,7 – 11,3 = 9,4.
Paso 6: Busque el valor de q en esta tabla . Con 2 tratamientos (ahora está excluyendo la media más alta, por lo que el valor q cambiará) y 6 grados de libertad para el término de error, el valor Q es 3,46.
Paso 7: Multiplique σd (Paso 4) por el nuevo valor q (Paso 6):
2,42 * 3,46 = 8,37.
La diferencia entre la segunda media más alta y la más baja es superior a 8,37, por lo que la segunda media más alta difiere significativamente de la media más baja.
Si tiene más valores en su tabla, continúe hacia abajo en su tabla, cambiando el valor q a medida que avanza. Una vez que tenga un resultado no significativo, puede detenerse en ese punto.
Redactor del artículo
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
