Actualizado por ultima vez el 31 de enero de 2022, por Luis Benites.
La significación estadística es una forma de decirle si los resultados de su prueba son sólidos. La estadística no es una ciencia exacta. De hecho, puedes pensar en las estadísticas como conjeturas muy precisas. Como las estadísticas son conjeturas, necesitamos saber qué tan cerca está nuestra «suposición». Ahí es donde entra la importancia.
Qué es la significación estadística: descripción general
Las estadísticas se tratan de tomar una parte de la población y adivinar cómo podría ser el comportamiento de esa población. Si estuviera trabajando con parámetros ( explicación de parámetro frente a estadística ), no habría necesidad de conjeturas; Tendrías todos los datos. En la vida real, obtener todos los datos puede ser costoso, lento o imposible .
Por ejemplo, Gallup Polls usa estadísticas para estimar quién ganará las próximas elecciones. Los fabricantes de medicamentos usan estadísticas para estimar cuántas personas podrían tener efectos secundarios a causa de sus medicamentos. Y las empresas usan estadísticas para pronosticar las cifras de ventas para el futuro.
¿De qué es la significación estadística una medida?
La importancia estadística es una medida de si los hallazgos de su investigación son significativos . Más específicamente, es si su estadística coincide con el valor que esperaría encontrar en una población completa . Como ejemplo simple, supongamos que trabaja para una empresa de encuestas y le pregunta a 120 personas cómo van a votar en las próximas elecciones. Le gustaría que su informe reflejara a todos en el país, ¿verdad? En otras palabras, desea que su informe tenga hallazgos significativos . ¿Cómo se mide la “significación”? Con algunos cálculos.
Para probar la significación estadística, realice estos pasos:
- Decidir sobre un nivel alfa . Un nivel alfa es la tasa de error con la que está dispuesto a trabajar (generalmente 5% o menos).
- Lleva a cabo tu investigación. Por ejemplo, realice una encuesta o recopile datos de un experimento.
- Calcula tu estadística . Una estadística es solo una pieza de información sobre su muestra, como una media , moda o mediana .
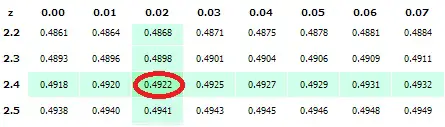
- Compare la estadística que calculó en el Paso 3 con una estadística de una tabla estadística .
¿ Necesita ayuda para elegir una prueba? ¡Mira nuestra página de tutoría!
Hay muchos tipos diferentes de tablas que puede usar para averiguar si sus datos tienen importancia estadística o no. Para obtener más información sobre las pruebas de hipótesis , consulte nuestro índice de Pruebas de hipótesis .
El significado limitado de la significación estadística
Cuando nuestra estadística de muestra está fuera de nuestro intervalo de confianza del 95% , rechazamos la hipótesis nula y llamamos al resultado estadísticamente significativo. ¿Qué significa «estadísticamente significativo»? Qué nos dice esto? Al principio, muchas personas piensan que un resultado estadísticamente significativo usando un intervalo de confianza del 95 % les dice que hay un 95 % de posibilidades de que sean correctos y un 5 % de posibilidades de que sean incorrectos. Pero, desafortunadamente, eso no es lo que significa. Su significado es mucho más limitado. Solo nos dice que hay un 95% de posibilidades de que estemos en lo correcto y un 5% de posibilidades de que estemos incorrectos cuando la hipótesis nula es verdadera. Es sobre esta base que rechazamos la Hipótesis Nula.
El significado de significancia estadística también está limitado de otra manera. Mucha gente piensa, al principio, que la significancia estadística les dice que los resultados deben tener implicaciones significativas en el mundo real, que los resultados son significativos en la práctica. Pero, desafortunadamente, eso tampoco es lo que significa. El término significativo se califica con el término estadísticamente. No significa significativo en general, significativo en la práctica o significativamente significativo.
Para ilustrar, veamos tres ejemplos de significación estadística. Todos implican calcular el intervalo del 95% que rodea a .5. Implican tamaños de muestra de 100, 1000 y 10,000. El intervalo del 95% se estrecha a medida que aumenta el tamaño de la muestra. En algún momento, el intervalo del 95% se reducirá a nada. En el caso de un tamaño de muestra de 10.000, el intervalo es muy estrecho. El margen de error es solo 0.01, o 1%. Si bien un tamaño de muestra de diez mil puede parecer ridículamente grande, en la era moderna de los «grandes datos» digitalizados, en realidad no lo es. De todos modos, el punto principal sigue siendo que con tamaños de muestra lo suficientemente grandes podemos hacer que casi cualquier resultado sea estadísticamente significativo.
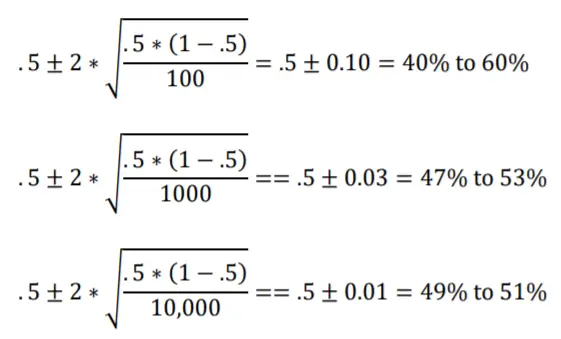
Entonces, si tuviéramos una muestra de diez mil y nuestro porcentaje de muestra fuera 51.1%, ¿qué inferiríamos? Bien, rechazaríamos la Hipótesis Nula de que la población está a favor en un 50%, y llamaríamos al resultado estadísticamente significativo. Porque es. Pero ¿qué pasa con el significado práctico? ¿Es el 51,1 % significativamente diferente del 50 % en términos de sus implicaciones prácticas? Tal vez tal vez no.
La significancia estadística es importante cuando se evalúan los resultados del análisis estadístico, pero también es necesario observar los valores estadísticos reales involucrados y decidir si son significativos en la práctica, con implicaciones significativas en el mundo real.
Y si bien queremos tener tamaños de muestra lo suficientemente grandes para evitar un riesgo indebido de error de tipo II, también debemos tener cuidado al usar tamaños de muestra tan grandes que los resultados insignificantes tienen importancia estadística. Aquí hay un ejemplo de eso: un estudio encontró que cierto suplemento dietético redujo el riesgo de contraer una cierta dolencia menor de 2 en 1000 (0.2%) a 1 en 1000 (0.1%). El tamaño de la muestra del estudio fue de 30.000, por lo que la diferencia entre el 0,2 % y el 0,1 % es estadísticamente significativa (al 95 % de confianza). Eso da una diferencia de riesgo relativo del 50 % (0,2 % – 0,1 %)/0,2 %), pero un riesgo absoluto diferencia de solo 0,1% (0,2% – 0,1%). Los anuncios del suplemento destacaban los hechos de que el efecto positivo del suplemento era estadísticamente significativo y que el suplemento reducía el riesgo de contraer la enfermedad en un 50 %, pero los anuncios no mencionaban que la reducción absoluta del riesgo era solo del 0,1 %. Mucha gente lo encontraría engañoso. Y muchas personas considerarían que una diferencia de riesgo absoluto del 0,1% es insignificante y prácticamente insignificante.
En pocas palabras : definitivamente desea conocer las diferencias relativas y absolutas para evaluar mejor el significado práctico.
El escándalo Vioxx: ¿Qué tan significativo es «significativo»?
Hace poco más de una década, tuve un trastorno raro que afectaba el cartílago de mi pecho, llamado Síndrome de Tietze. El síndrome de Tietze es una inflamación del cartílago costal, es extremadamente doloroso, y el tratamiento en ese momento, la “ medicina milagrosa ” del reumatismo de cualquier tipo, era una pastillita llamada Vioxx. Había un pequeño problema con Vioxx. El fabricante, Merck, utilizó estadísticas para ocultar el hecho de que el medicamento tenía un efecto secundario menor : provocaba ataques cardíacos. Afortunadamente, yo no fui uno de los desafortunados.
Vioxx es un tipo de medicamento antiinflamatorio no esteroideo (AINE), similar a la aspirina o al ibuprofeno. El fabricante, Merck, gastó millones (160 millones en 2000) en publicidad directa al consumidor del fármaco. El fármaco fue aprobado por la FDA en 1999 y retirado en 2004 después de una serie de demandas legales que afirmaron que el fármaco causó 23 800 eventos cardiovasculares (incluidos ataques cardíacos) y un estudio de 2004 (APPROVe) que encontró un exceso estadísticamente significativo de eventos cardiovasculares en pacientes con Vioxx en comparación con los pacientes de placebo.
El escándalo Vioxx: ¿Qué pasó?
¿Entonces qué pasó? ¿Cómo podría un fármaco tener importancia estadística, ser aprobado por la FDA y comercializarse si el fármaco no era seguro? La respuesta es que cuando se publicaron los estudios originales sobre el fármaco, varios de los autores de Merck no incluyeron tres infartos de miocardio (ataques cardíacos) en la revisión final del artículo. Sabían sobre los ataques cardíacos, pero también sabían que incluir esos tres casos lo haría lo suficientemente significativo estadísticamente como para que el medicamento no fuera aprobado. Tres casos lavados debajo de la alfombra fueron suficientes para convertir un evento estadísticamente insignificante (es decir, el medicamento fue aprobado) a uno significativo (el medicamento no habría sido aprobado).
Solo puedo imaginar lo que sucedió en Merck y la presión que tuvieron estos científicos para «olvidar» esos tres casos después de que Merck hubiera gastado millones en desarrollo (sin mencionar los miles de millones que obtendrían de las ventas). Lo más probable es que los científicos (o sus jefes) no entendieron el significado de estadísticamente significativo , porque no puedo imaginar que pensaran que ocultar tres casos en una muestra provocaría decenas de miles de ataques cardíacos en la población.
Referencias
Gonick, L. (1993). La guía de dibujos animados de estadísticas . Harper Perennial.
Kotz, S.; et al., editores. (2006), Enciclopedia de Ciencias Estadísticas , Wiley.
Krumholz et al. (2007). ¿Qué hemos aprendido de Vioxx? BMJ. 2007 20 de enero; 334 (7585): 120–123.
Referencias
JE Kotteman. Análisis Estadístico Ilustrado – Fundamentos . Publicado vía Copyleft . Usted es libre de copiar y distribuir el contenido de este PDF.

