Actualizado por ultima vez el 17 de septiembre de 2021, por Luis Benites.
¿Qué es el rastro de Pillai?
La traza de Pillai se utiliza como estadística de prueba en MANOVA y MANCOVA . Esta es una estadística de valor positivo que va de 0 a 1. Los valores crecientes significan que los efectos están contribuyendo más al modelo; debe rechazar la hipótesis nula para valores grandes.
Pillai’s es una de varias estadísticas de prueba utilizadas en MANOVA; Otras pruebas comúnmente utilizadas incluyen: T 2 de Hotelling , raíz más grande de Roy, raíz más grande de Roy (Criterio): Definición y Lambda de Wilks ).
Cuándo usar esta prueba
Esta prueba se considera la estadística más poderosa y robusta para uso general, especialmente para las desviaciones de los supuestos. Por ejemplo, si se viola la suposición MANOVA de homogeneidad de varianza-covarianza, la de Pillai es su mejor opción. También es una buena opción cuando tiene tamaños de celda desiguales o tamaños de muestra pequeños (es decir, cuando n es pequeño).
Sin embargo, cuando los grados de libertad de la hipótesis son mayores que uno, el de Pillai tiende a ser menos poderoso que los otros tres. Si tiene una gran desviación de la hipótesis nula o los valores propios tienen grandes diferencias, la raíz máxima de Roy es una opción mucho mejor (Seber 1984).
Fórmula
La fórmula para la traza de Pillai es: Los pasos generales para calcular el estadístico de prueba son:
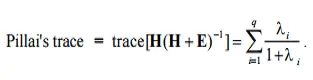
- Divide cada valor propio por 1 + la raíz característica.
- Suma estas proporciones.
Es extremadamente raro que desee realizar estos cálculos a mano; La mayoría de los paquetes estadísticos realizarán los cálculos por usted como parte de MANOVA o MANCOVA. La salida devolverá un valor de seguimiento de Pillai, una estadística F asociada y un valor p . En general, los valores de p pequeños (por debajo de .05) significan que Pillai arrojó un resultado significativo (que hay una diferencia entre los niveles de la variable independiente que está viendo).
Referencias :
Pillai KCS (1955). Algunos nuevos criterios de prueba en el análisis multivariante . Ann Math Stat: 26(1):117–21.
Seber, GAF (1984). Observaciones multivariadas . Nueva York: John Wiley and Sons

