Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 23 de febrero de 2022, por Luis Benites.
La relación de verosimilitud monótona (MLR) representa un proceso útil de generación de datos; uno en el que existe una relación clara entre la magnitud de las variables observadas y la distribución de probabilidad de la que se extraen. Esta clara relación hace posibles muchos procesos estadísticos, incluida la identificación uniforme de los procesos más poderosos .
El MLR se define de la siguiente manera:
Si la razón de las dos funciones de densidad de probabilidad, f(x) y g(x) cumplen el siguiente requisito, tienen la propiedad de razón de verosimilitud monótona: La razón nunca disminuye para todo X .
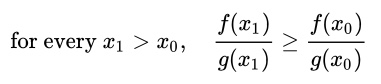
Fraseología
Si, con respecto a un argumento particular x, dos funciones cumplen la condición anterior, diríamos que «tienen la propiedad de razón de verosimilitud monótona en x». Cuando una familia de distribuciones tiene razones de verosimilitud monótonas con respecto a un estadístico T(X), diríamos que la familia ‘tiene la propiedad MLR en T(X)’.
Familias de distribuciones que satisfacen la MLR
Las siguientes familias satisfacen la propiedad de razón de verosimilitud monótona para el estadístico T(X)= Σ:
- Distribuciones exponenciales [λ]
- Distribuciones binomiales [n, p],
- Distribuciones de Poisson [λ],
- Distribución normal [μ, σ] si se conoce σ.
Importancia de la propiedad de la razón de verosimilitud monótona
La propiedad MLR es importante en áreas como: modelos de probabilidad, prueba de hipótesis y estimación puntual . Esta propiedad también se utiliza para derivar pruebas Uniformly Most Powerful (UMP) para la prueba de hipótesis. Una UMP es una prueba que tiene la mayor potencia entre todas las pruebas posibles de un tamaño determinado; por lo que determinar cuál es en una circunstancia dada puede ser muy importante.
Referencias
- Razón de verosimilitud monótona. Estadísticas para aplicaciones: notas de conferencias de otoño de 2003. https://ocw.mit.edu/courses/mathematics/18-443-statistics-for-applications-fall-2003/lecture-notes/lec21.pdf el 3 de mayo de 2018.
- Mukherjee, Shirsendu. Inferencia Estadística I: Razón de Verosimilitud Monótona. Recuperado de http://epgp.inflibnet.ac.in/epgpdata/uploads/epgp_content/S000034ST/P001013/M020980/ET/1499856024Module-31.pdf el 3 de mayo de 2018
- Watkins, J. Pruebas uniformemente más poderosas. Obtenido de http://math.arizona.edu/~jwatkins/ump.pdf el 3 de mayo de 2018.
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
