Actualizado por ultima vez el 25 de septiembre de 2021, por Luis Benites.
Es posible que desee leer sobre la regularización y la reducción antes de leer este artículo.
¿Qué es la regresión de lazo?
La regresión de lazo es un tipo de regresión lineal que utiliza la contracción . La reducción es donde los valores de los datos se reducen hacia un punto central, como la media . El procedimiento de lazo fomenta modelos simples y dispersos (es decir, modelos con menos parámetros). Este tipo particular de regresión es adecuado para modelos que muestran altos niveles de multicolinealidad o cuando desea automatizar ciertas partes de la selección del modelo, como la selección de variables/eliminación de parámetros.
El acrónimo “LASSO” significa Operador de selección y reducción absoluta mínima .
Regularización L1
La regresión de Lasso realiza la regularización L1 , que agrega una penalización igual al valor absoluto de la magnitud de los coeficientes. Este tipo de regularización puede resultar en modelos dispersos con pocos coeficientes; Algunos coeficientes pueden convertirse en cero y eliminarse del modelo. Las penalizaciones más grandes dan como resultado valores de coeficiente más cercanos a cero, lo cual es ideal para producir modelos más simples. Por otro lado, la regularización de L2 (por ejemplo , la regresión de Ridge ) no da como resultado la eliminación de coeficientes o modelos dispersos. Esto hace que Lasso sea mucho más fácil de interpretar que Ridge.
Realización de la regresión
Las soluciones de Lasso son problemas de programación cuadrática, que se resuelven mejor con software (como Matlab ). El objetivo del algoritmo es minimizar: Que es lo mismo que minimizar la suma de cuadrados con la restricción Σ |B j ≤ s (Σ = notación de suma ). Algunas de las β se reducen a exactamente cero, lo que da como resultado un modelo de regresión que es más fácil de interpretar.
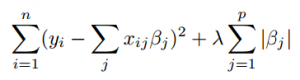
Un parámetro de ajuste , λ controla la fuerza de la penalización L1. λ es básicamente la cantidad de contracción:
- Cuando λ = 0, no se elimina ningún parámetro. La estimación es igual a la encontrada con la regresión lineal.
- A medida que λ aumenta, más y más coeficientes se ponen a cero y se eliminan (teóricamente, cuando λ = ∞, se eliminan todos los coeficientes).
- A medida que aumenta λ, aumenta el sesgo .
- A medida que λ disminuye, la varianza aumenta.
Si se incluye una intersección en el modelo, por lo general no se modifica.
Referencias
Beyer, WH CRC Standard Mathematical Tables, 31ª ed. Boca Raton, FL: CRC Press, págs. 536 y 571, 2002.
Agresti A. (1990) Análisis de datos categóricos. John Wiley and Sons, Nueva York.
Kotz, S.; et al., editores. (2006), Enciclopedia de Ciencias Estadísticas , Wiley.
Wheelan, C. (2014). Estadísticas desnudas . WW Norton y compañía

