Actualizado por ultima vez el 22 de febrero de 2022, por Luis Benites.
La regresión sinusoidal encuentra un modelo trigonométrico que proporciona la curva de mejor ajuste. La idea es la misma que encontrar la línea de mejor ajuste en una regresión lineal . Sin embargo, en lugar de encontrar una línea recta, esta vez encontrarás una curva sinusoidal.
Mire el video para obtener una descripción general y cómo hacer una regresión sinusoidal en Desmos.com o en la TI-83:
Regresión sinusoidal (Desmos y TI-83) 
Mira este video en YouTube .
¿No puedes ver el vídeo? Haga clic aquí
Los datos que se ajustan a una curva de regresión sinusoidal tienden a fluctuar con el tiempo en curvas onduladas u onduladas. Por ejemplo, las temperaturas de un año a otro tienden a ondular en un patrón sinusoidal. Las ondas sinusoidales también se ven comúnmente en el procesamiento de señales y el análisis de series temporales.
Crear un diagrama de dispersión siempre es una buena idea antes de realizar cualquier tipo de regresión, ya que normalmente obtendrá un resultado incluso si sus datos son completamente inapropiados para el tipo de regresión que está ejecutando. Por ejemplo, si sus puntos de datos se ajustan a una línea recta, una regresión sinusoidal le dará un resultado, pero la ecuación de regresión será completamente inútil para realizar pronósticos.
Ejemplo de regresión sinusoidal
Este ejemplo utiliza este conjunto de datos meteorológicos de Desmo.com para una ubicación ficticia.
Paso 1: crea un diagrama de dispersión . Puede cambiar los puntos de entrada de datos en la tabla de la izquierda escribiendo las entradas (tal como lo haría en una hoja de cálculo): Podemos ver que una curva sinusoidal, u onda, sería una buena opción para estos datos, por lo que podemos Seguir.
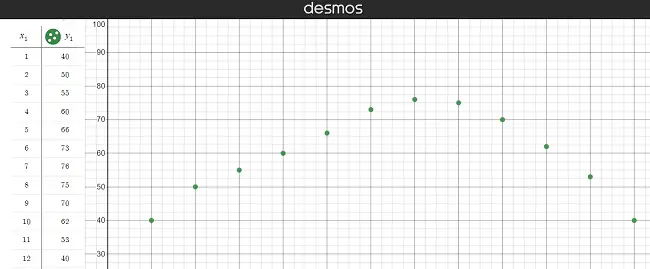
Paso 2: Elija una función seno o una función coseno . El término “sunusoidal” se refiere a ambos tipos, por lo que debe elegir uno u otro.
- Si su diagrama de dispersión (del Paso 1) muestra un pico en x = 0, elija la función coseno.
- Si su gráfico de dispersión está compensado, con el pico más cerca de 1, elija la función seno.
Tenga en cuenta que este es solo un punto de partida; La principal diferencia entre el seno y el coseno es que el gráfico del seno es el gráfico del coseno desplazado hacia la derecha en el eje x en π/2 unidades [1]. Puede intentar colocar uno o ambos: hay mucho margen de maniobra y no puede tomar una decisión equivocada, como verá en los siguientes pasos.
El ejemplo en el conjunto de datos de Desmos es la función SIN. Las estadísticas de regresión se actualizarán automáticamente cuando ingrese nuevos datos en la tabla.
Paso 3: Introduce tus resultados en la ecuación
y = a * sin(bx + c) + d.
Para este ejemplo, obtenemos los siguientes resultados: Conectándolos, obtenemos (redondeado a dos decimales): y = 18,99 * sin(0,43x + 3,30) + 56,29.
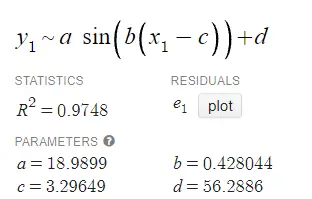
Aquí, las diferentes partes de la ecuación son:
- a = amplitud
- 2π/b es el periodo
- c = cambio de fase
- d = desplazamiento vertical.
Paso 4: Verifique que su ecuación de regresión se ajuste a la curva escribiendo la función en Desmos. Escribir y = 18,99 * sin(0,43x + 3,30) + 56,29 te da una curva de compensación. Sabemos que cos se compensa con π/2, por lo que cambiar sen por cos da el ajuste correcto: y = 18,99 * cos(0,43x + 3,30) + 56,29.
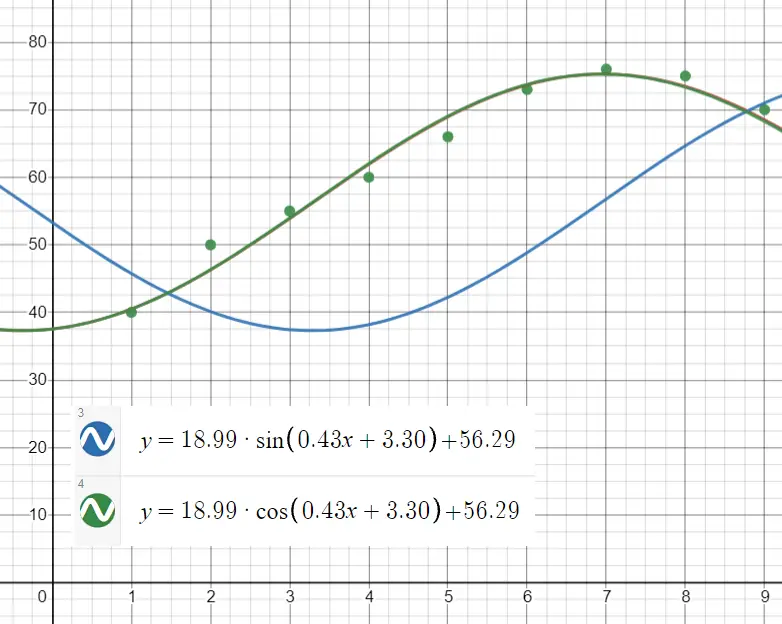
La onda sinusoidal (azul) está compensada; la onda coseno (verde) da un mejor ajuste.
Regresión sinusoidal TI-83
Si tiene una calculadora TI-83, puede realizar una regresión sinusoidal con la función SinReg en el menú STATS. Los pasos básicos están a continuación (o vea el video en YouTube ):
- Pulse STAT.
- Asegúrese de que EDIT esté resaltado en la fila superior, luego presione ENTER.
- Escriba sus valores de x en L1, luego escriba sus valores de y en L2.
- Desde la pantalla de INICIO, presione STAT nuevamente.
- Use el cursor para resaltar CALC en la parte superior de la pantalla.
- Flecha hacia abajo hasta C:SinReg, luego presione ENTER dos veces.
- Siga el Paso 3 anterior para conectar sus resultados en la ecuación.
Referencias
[1]Hallman, A. Exploraciones con seno y coseno . Recuperado el 4 de octubre de 2021 de: http://jwilson.coe.uga.edu/EMAT6680Fa07/Hallman/Assigment%201/assignment1-allyson.html
