Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 26 de febrero de 2022, por Luis Benites.
¿Cuál es la g de Hedges?
La g de Hedges es una medida del tamaño del efecto . El tamaño del efecto le dice cuánto difiere un grupo de otro, generalmente una diferencia entre un grupo experimental y un grupo de control .
La g de Hedges y la d de Cohen son extremadamente similares. Ambos tienen un sesgo al alza (una inflación) en los resultados de hasta alrededor del 4%. Las dos estadísticas son muy similares, excepto cuando los tamaños de muestra están por debajo de 20, cuando la g de Hedges supera a la d de Cohen. Por lo tanto, g de Hedges a veces se denomina tamaño del efecto corregido.
- Para tamaños de muestra muy pequeños (<20) elija la g de Hedges sobre la d de Cohen.
- Para tamaños de muestra >20, los resultados de ambas estadísticas son aproximadamente equivalentes.
- Si las desviaciones estándar son significativamente diferentes entre los grupos, elija el delta de Glass en su lugar. El delta de Glass usa solo la desviación estándar del grupo de control (SD C ).
Fórmula
La fórmula g de Hedge es: Donde :
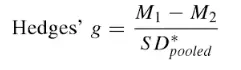
- M 1 – M 2 = diferencia de medias.
- SD* agrupado = desviación estándar agrupada y ponderada .
¿ Necesitas ayuda con la fórmula? ¡Mira nuestra página de tutoría!
La principal diferencia entre la g de Hedge y la D de Cohen es que la g de Hedge utiliza desviaciones estándar ponderadas combinadas (en lugar de desviaciones estándar combinadas).
Una nota sobre los tamaños de muestra pequeños:
la g de Hedges (como la d de Cohen) está sesgada hacia arriba para muestras pequeñas (menos de 50). Para corregir esto, use la siguiente fórmula:
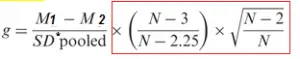
Interpretación de resultados
Una g de 1 indica que los dos grupos difieren en 1 desviación estándar, una g de 2 indica que difieren en 2 desviaciones estándar y así sucesivamente. Las desviaciones estándar son equivalentes a las puntuaciones z (1 desviación estándar = 1 puntuación z).
Interpretación de la regla general
La d de Cohen y la g de Hedges se interpretan de manera similar. Cohen sugirió usar la siguiente regla general para interpretar los resultados:
- Efecto pequeño (no se puede discernir a simple vista) = 0,2
- Efecto Medio = 0.5
- Efecto grande (se puede ver a simple vista) = 0,8
Cohen sugirió precaución al usar esta regla general. Los términos efectos “pequeños” y “grandes” pueden tener diferentes significados en diferentes áreas. Por ejemplo, una reducción «pequeña» en las tasas de suicidio es invaluable, mientras que una pérdida de peso «pequeña» puede no tener sentido. Durlak (2009) sugiere consultar estudios previos para ver dónde encajan sus resultados en el panorama general.
Referencias :
Cohen, J. (1977). Análisis de poder estadístico para las ciencias del comportamiento . Routledge.
Durlak, J. (2009) Cómo seleccionar, calcular e interpretar los tamaños de los efectos. Revista de Psicología Pediátrica. Marzo: 34(9):917-28.
Ellis, P. (2010). La guía esencial para los tamaños del efecto: poder estadístico, metanálisis y la interpretación de los resultados de la investigación .
Coberturas, L. (1981). Teoría de distribución para el estimador de tamaño del efecto de Glass y estimadores relacionados. Revista de Estadística Educativa. vol. 6, No. 2 (verano de 1981), págs. 107-128. Todo el PDF disponible de forma gratuita en JSTOR .
Coberturas LV, Olkin I. (1985). Métodos estadísticos para metanálisis . San Diego, CA: Prensa académica
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
