Actualizado por ultima vez el 18 de octubre de 2021, por Luis Benites.
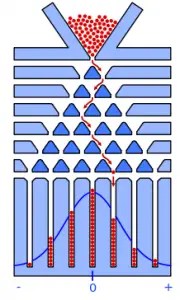El tablero de Galton (también llamado Quincunx) es un modelo físico de la distribución binomial que ilustra bellamente el teorema del límite central ; Cuando agrega variables aleatorias independientes , su suma tiende hacia una distribución normal . En particular, demuestra que la distribución binomial es aproximadamente una distribución normal.
Inventado por Sir Francis Galton (1822-1911), el tablero Galton es un tablero rectangular colocado verticalmente con clavijas o clavos espaciados uniformemente (representados por triángulos en la imagen) sobre su mitad superior. Un embudo con una ranura lo suficientemente grande como para dejar salir una bola a la vez se coloca cerca de la parte superior. En la mitad inferior del tablero hay ranuras rectangulares, cada una del mismo ancho que las bolas que se utilizarán para el experimento. El embudo se coloca de modo que una bola que pase por él golpee uno de los clavos de la primera fila directamente en el centro.
Por lo general, se coloca una cubierta de vidrio sobre toda la configuración para observar el progreso de las bolas a través del embudo.
Dónde encontrar tableros Galton
Soy dueño de esta excelente placa Galton de la editorial Four Pines.
Es uno de los Galton Board más económicos del mercado, pero está bien hecho y viene empacado en una elegante caja profesional. Además de ser un dispositivo de escritorio algo adictivo, también demuestra otros conceptos, incluido el Triángulo de Pascal y la regresión a la media .
Recomiendo encarecidamente este producto para su salón de clases, su escritorio o como regalo para su matemático favorito. ¡Consigue el tuyo en Amazon y el envío es gratis!
Ejecución de una demostración de la placa Galton
Para realizar un experimento que demuestre la forma de la distribución binomial, se debe colocar una gran cantidad de bolas en el embudo y dejar que corran hacia el tablero perforado que se encuentra debajo. Cada bola, a medida que cae, golpeará el clavo debajo del embudo y rebotará hacia la izquierda o hacia la derecha— Entonces p l = 1- p r . En otras palabras, la probabilidad de que una pelota vaya hacia la izquierda (p l ) es 1 menos la probabilidad de que una pelota vaya hacia la derecha (p r ). Si las clavijas están dispuestas simétricamente, p l = p r = ½.
Estas bolas seguirán rebotando contra las clavijas de abajo. En cada clavija, la bola ‘escogerá’ aleatoriamente una de dos direcciones, izquierda o derecha, para rodearla. Eventualmente, cada bola caerá en una de las ranuras en la parte inferior.
Cada paso es aleatorio, por lo que si la pelota golpea n clavijas en su viaje descendente, la ranura en la que finalmente termina se puede considerar como la suma de n variables aleatorias . Como el teorema del límite central nos dice que la suma de k variables aleatorias se aproxima a una distribución normal a medida que k aumenta, podemos esperar que la distribución en nuestras ranuras sea normal. Deberíamos ver una gran «campana» o protuberancia en el centro del tablero, que se estrecha en ambos bordes. Esta distribución se acercará cada vez más a la normal cuanto mayor sea el número de clavijas que tenga nuestro tablero y cuanto mayor sea el número de bolas que se dejen caer.
Referencias
Starnes, D. (2009). Estadísticas a través de aplicaciones. Macmillan.
Quincunx Applet y el teorema del límite central. Recuperado de
http://www.stat.ucla.edu/~dinov/courses_students.dir/Applets.dir/QuincunxApplet.html el 30 de noviembre de 2017
