Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 18 de octubre de 2021, por Luis Benites.
La distribución muestral de la proporción de la población le brinda información sobre la proporción de la población , p. Por ejemplo, es posible que desee saber la proporción de la población (p) que usa Facebook. No puede encuestar a todos en el planeta, por lo que usa una muestra y obtiene la proporción de muestra p̄ y la usa como estimador para p.
Al estudiar la distribución muestral de la proporción muestral, también verá una p minúscula. La versión en minúsculas se refiere a un solo valor (es decir, una sola estimación).
Mire el video para ver un ejemplo del valor esperado y las fórmulas de error estándar para la proporción de la muestra.
Valor esperado y error estándar para la proporción de la muestra Mira este video en YouTube .
¿No puedes ver el vídeo? Haga clic aquí
Fórmulas útiles para la distribución muestral de la proporción muestral
- Valor esperado de la distribución muestral de P̄:
E(p̄) = p. - Varianza para la distribución muestral de P̄:
p(1-p) / n. - Error Estándar (SE) de la Proporción Muestral:
√ (p(1-p) / n). Nota : a medida que aumenta el tamaño de la muestra , el error estándar disminuye. - Puede usar la distribución normal si las siguientes dos fórmulas son verdaderas:
- np≥5
- n(1-p)≥5.
- Puntuación Z para la proporción de la muestra: z = (P̄ – p) / SE
Proporción muestral y el teorema del límite central
En la mayoría de los libros de estadística (y en la vida real), realmente solo hará inferencias sobre las proporciones de la población si tiene un tamaño de muestra lo suficientemente grande. Si tiene un tamaño de muestra lo suficientemente grande, puede usar la distribución normal para la distribución de muestreo de P̂.
¿Qué tan grande es «suficientemente grande»? Utilice estas fórmulas como guía general:
- np≥5
- n(1-p)≥5.
Por ejemplo, si tuviera un tamaño de muestra (n) de 50 y una proporción de 30%, entonces:
n * p = 50 * .3 = 15
50(1-.3) = 50(.7) = 35.
Estos son mayores que 5, por lo que puede usar la distribución normal.
Puede transformar P̄ en una puntuación z con la siguiente fórmula:
Puntuación Z para proporción de muestra: z = (p̄ – p) / SE.
Ejemplo de pregunta:
Los clientes de una determinada empresa están compuestos por un 43 % de mujeres y un 57 % de hombres. Una campaña de marketing agresiva da como resultado un aumento de clientes mujeres al 46%, según una encuesta de muestra de 50 clientes. Si la empresa no hubiera realizado la campaña, ¿cuál es la probabilidad de que el 46 % de los clientes sean mujeres? ¿Valió la pena la campaña?
Tenga en cuenta que está buscando la probabilidad de que P̄ sea mayor o igual al 46 %.
Solución:
Paso 1: Verifique que el tamaño de su muestra sea lo suficientemente grande:
n * p = 50 * .43 = 21.5
50(1-.43) = 28.5.
Ambos están por encima de 5, por lo que podemos usar la distribución normal.
Paso 2: Encuentra el error estándar (SE):
√ (p(1-p) / n) = √ (0.43(1-0.43) / 50) = 0.07.
Paso 3: Encuentre el puntaje z, usando el SE que calculó en el Paso 2:
z = (P̄ – p) / SE
P(Z≥) (0.46 – 0.43)/0.07 = 0.43.
Paso 4: Busque 0.43 en la tabla z . La probabilidad es 0,3336 o 33,36%.*
Con una probabilidad del 33,36 %, es bastante probable que la proporción de mujeres hubiera sido del 46 % sin una campaña. Es poco probable que la campaña de marketing haya marcado una gran diferencia.
*Cómo calculé esto:
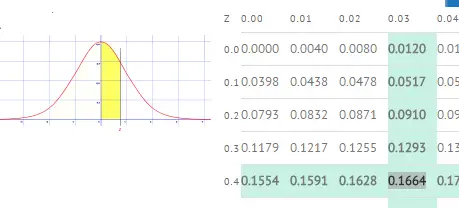
- Encontré un valor de 0.1664 en la tabla z. Esta es el área entre la media y z (en amarillo).
- Como quiero el área de la cola (mayor que z), resté del 50% (es decir, la mitad de la curva). Si hubiera estado usando una tabla z completa (de -3 a 3 desviaciones estándar), habría restado de 1.
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
