Contenido de este artículo
Actualizado el 8 de diciembre de 2021, por Luis Benites.
La varianza de la población (σ 2 ) nos dice cómo se distribuyen los puntos de datos en una población específica. Es el promedio de las distancias de cada punto de datos en la población a la media, al cuadrado.
σ 2 generalmente se representa como σ 2 y se puede calcular usando la siguiente fórmula: Aquí N es el tamaño de la población y x i son puntos de datos. μ es la media de la población .
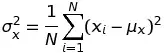
Ejemplo
Ejemplo de pregunta: Encuentre la varianza poblacional de la edad de los niños en una familia de cinco niños de 16, 11, 9, 8 y 1 años:
Paso 1: Encuentra la media , μ x :
μ = 9.
Paso 2: reste cada punto de datos de la media, luego eleve al cuadrado el resultado:
(16-9) 2 = 49
(11-9) 2 = 4
(9-9) 2 = 0
(8-9) 2 = 1
(1 -9) 2 = 64.
Paso 3: Sume todas las diferencias al cuadrado del Paso 2:
(16-9) 2 + (11-9) 2 + (9-9) 2 + (8-9) 2 + (1-9) 2 = 118 .
Paso 4: Divida el Paso 3 por el número de artículos. 118/5 da una varianza de población de 23,6.
Propiedades de la varianza de la población
Dado que las medidas de la varianza de la población se dispersan, σ 2 para un conjunto de puntos idénticos es 0.
Si agrega una constante a cada punto de datos, el σ 2 permanece sin cambios. Por ejemplo, suponga que estudia los años de nacimiento de las personas mayores en Nueva York y decide cambiar los calendarios del gregoriano estándar a un calendario donde 1900 era el año 1, el σ 2 permanecería igual.
La raíz cuadrada de la varianza de la población es la desviación estándar de la población, que representa la distancia promedio desde la media.
La varianza de la población es un parámetro de la población y no depende de los métodos de investigación ni de las prácticas de muestreo.
Diferencias entre la varianza de la población y la varianza de la muestra
La varianza de la muestra es una estimación de σ 2 y es muy útil en situaciones en las que calcular la varianza de la población sería demasiado engorroso. Las únicas diferencias en la forma en que se calcula la varianza de la muestra es que se usa la media de la muestra , las desviaciones se suman sobre la muestra y la suma se divide por n-1 ( ¿Por qué usar n-1? ). Al calcular la varianza de la muestra, n es el número de puntos de muestra (frente a N para el tamaño de la población en la fórmula anterior).
A diferencia de la varianza de la población, la varianza de la muestra es simplemente una estadística de la muestra. Depende de la metodología de investigación y de la muestra elegida. Es probable que una nueva muestra o un nuevo experimento le proporcionen una varianza de muestra diferente, aunque si ambas muestras son representativas, sus varianzas de muestra deberían ser buenas estimaciones de la varianza de la población y muy cercanas entre sí.
Fuentes
Referencias
Beyer, WH CRC Standard Mathematical Tables, 31ª ed. Boca Ratón, FL: CRC Press, págs. 536 y 571, 2002.
Gonick, L. (1993). La guía de dibujos animados de estadísticas . Harper Perennial.
Kotz, S.; et al., editores. (2006), Enciclopedia de Ciencias Estadísticas , Wiley.
Vogt, WP (2005). Diccionario de estadística y metodología: una guía no técnica para las ciencias sociales . SABIO.
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:

no entendi su utilidad