Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 28 de octubre de 2021, por Luis Benites.
La asimetría del modo de Pearson, también llamado primer coeficiente de asimetría de Pearson , es una forma de determinar la asimetría de una distribución.
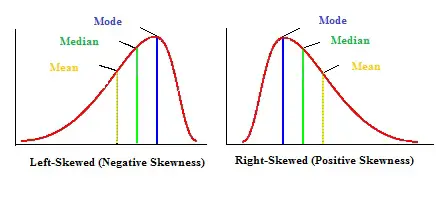
La media, la moda y la mediana se pueden usar para determinar si tiene una distribución sesgada positiva o negativamente.
- Si la media es mayor que la moda, la distribución tiene un sesgo positivo.
- Si la media es menor que la moda , la distribución tiene un sesgo negativo .
- Si la media es mayor que la mediana , la distribución tiene un sesgo positivo.
- Si la media es menor que la mediana, la distribución tiene un sesgo negativo.
Sesgo del modo de Pearson
La asimetría del modo de Pearson utiliza los hechos anteriores para ayudarlo a averiguar si tiene una asimetría positiva o negativa. Si tiene una distribución y conoce la media, la moda y la desviación estándar (σ), entonces la fórmula de asimetría de la moda de Pearson es:
(modo medio)/σ
Problema de ejemplo: tiene datos con una media de 19, una moda de 20 y una desviación estándar de 25. ¿Qué le dice la asimetría de la moda de Pearson sobre la distribución?
(moda media)/σ = (19-20)/25 = -0,04.
Hay un sesgo negativo muy leve (-0,04). Nota : para la mayoría de las intenciones y propósitos, esto contaría como una distribución simétrica ya que la asimetría es muy pequeña.
Asimetría del modo de Pearson: fórmula alternativa.
Si no conoce el modo, no podrá utilizar la asimetría del modo Pearson. Sin embargo, la dirección del sesgo también se puede averiguar encontrando dónde están la media y la mediana . Según Business Statistics , esto conduce a una segunda fórmula equivalente:
3(Media – Mediana) / σ
Esta fórmula también se denomina segundo coeficiente de asimetría de Pearson.
Asimetría del modo de Pearson: qué significan los resultados.
La diferencia entre la media y la moda, o la media y la mediana, le dirá cuánto se aleja la distribución de la simetría . Una distribución simétrica (por ejemplo, la distribución normal ) tiene una asimetría de cero.
Ambas ecuaciones dan resultados en desviaciones estándar , que son unidades de medida adimensionales de la media.
Referencias
Esquivar, Y. (2008). La Enciclopedia Concisa de Estadística . Saltador.
Gonick, L. (1993). La guía de dibujos animados de estadísticas . Harper Perennial.
Klein, G. (2013). La caricatura Introducción a la estadística. Colina y Wamg.
Vogt, WP (2005). Diccionario de estadística y metodología: una guía no técnica para las ciencias sociales . SABIO.
Redactor del artículo
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
