Actualizado por ultima vez el 11 de septiembre de 2021, por Luis Benites.
El coeficiente gamma (también llamado estadística gamma, o gamma de Goodman y Kruskal ) nos dice qué tan cerca «coinciden» dos pares de puntos de datos. Gamma prueba una asociación entre puntos y también nos dice la fuerza de la asociación. El objetivo de la prueba es poder predecir dónde se clasificarán los nuevos valores. Por ejemplo, si el puntaje A obtiene un puntaje «BAJO» para la pregunta 1 y «Alto» para la pregunta 2, ¿el puntaje B también resultará en una respuesta BAJA/Alta?
Gamma se puede calcular para variables ordinales (ordenadas) que son variables continuas (como altura o peso) o variables discretas (como «caliente», «más caliente» y «más caliente»). Si bien hay otros coeficientes que pueden calcular relaciones para este tipo de variables, como la D de Somer o la Tau de Kendall , generalmente se prefiere la gamma de Goodman y Kruskal cuando se tienen muchos rangos empatados. También es particularmente útil cuando sus datos tienen valores atípicos , ya que no afectan mucho los resultados. Para algunos campos de estudio, puede ser el método preferido para todos los datos ordinales dispuestos en una tabla bivariada . si tienes dos variables dicotómicas (por ejemplo, respuestas que son sí/no), use la Q de Yule en su lugar.
Rango del Coeficiente Gamma
El coeficiente gamma oscila entre -1 y 1.
- 1 = correlación positiva perfecta: si un valor sube, el otro también.
- -1 = correlación inversa perfecta: cuando un valor sube, el otro baja.
- 0 = no hay asociación entre las variables
Cuanto más se acerque a un 1 (o -1), más fuerte será la relación. Puede deducir la importancia de su resultado ejecutando una prueba de importancia para gamma (ver más abajo). Pero la solidez que deben tener estas relaciones depende del campo de estudio en el que esté trabajando. Por ejemplo, un .75 podría ser «lo suficientemente fuerte» en un campo, mientras que otro podría requerir más de .8.
Puede interpretar gamma como la proporción de pares clasificados de acuerdo. Por ejemplo, si gamma = +1, significa que todos los pares de su experimento están de acuerdo, o que todos los evaluadores acordaron en qué orden se deben clasificar los elementos.
Gamma trata las variables de forma simétrica; no tiene que formular hipótesis sobre cuáles podrían ser variables dependientes y cuáles independientes .
Cálculo del coeficiente gamma
La gamma de Goodman y Kruskal utiliza la siguiente fórmula: Donde:
![]()
- N c es el número total de pares que tienen el mismo rango ( pares concordantes )
- N d es el número de pares que no tienen el mismo rango ( pares discordantes ).
Ejemplo 1 (Simple 2×2)
Suponga que está analizando datos sobre las horas dedicadas al estudio en comparación con los puntajes de las pruebas. Puede plantear la hipótesis de que más estudio conducirá a mejores calificaciones , y recopila datos que podrían demostrarlo. Para hacerlo simple, definirá el estudio mínimo como menos de una hora a la semana y el estudio extensivo como algo más que eso. También definirá las buenas calificaciones como A y A+, y las malas calificaciones serán cualquier valor inferior. Puede tabular sus datos hipotéticos de esta manera: Las celdas ayd (tiempo mínimo/puntuaciones malas y tiempo extenso/puntuaciones buenas) son las que respaldan su hipótesis (es decir, son concordantes). Las celdas b y c van en la otra dirección; Si son significativos, van en contra de su hipótesis y no son de apoyo (discordantes).
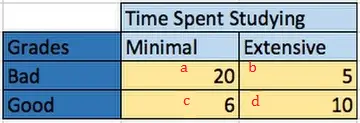
Para calcular el coeficiente gamma:
- Encuentre el número de pares concordantes, N c Comience con el cuadrado superior izquierdo y multiplique por la suma de todos los cuadrados concordantes de abajo ya la derecha (en este caso, solo d). norte c = 10 * 20 = 200,
- Encuentra el número de pares discordantes. N d se calcula de la misma manera; ahora, comience con el cuadrado superior derecho y multiplíquelo por la suma de todos los cuadrados ‘no complementarios’ de abajo ya la derecha. Haga esto nuevamente para cada cuadrado que no sea de apoyo , trabajando hacia abajo y hacia la izquierda.
norte re = 5 * 6 = 30. - Inserte los valores del Paso 1 en la fórmula:
La estadística gamma es:
(N c – N d ) / (N c + N d ) =
(200 – 30) / (200 + 30), o 0.7391.
Dado que el coeficiente gamma está mucho más cerca de 1 (correlación perfecta) que de 0 (sin asociación), sus datos apuntan a una fuerte correlación y su hipótesis tiene buenas posibilidades de ser correcta.
Ejemplo 2 (Complejo)
Esto funciona con una tabla más complicada: como antes, encuentre N c multiplicando cada celda por las sumas de las celdas y luego sumando esas sumas. La identificación de las celdas que necesitará en la ecuación se explica más fácilmente en un ejemplo paso a paso.
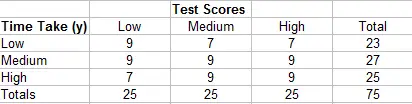
- Comience con la celda superior izquierda (9). Las celdas debajo y a la derecha son 9,9,9 y 9.
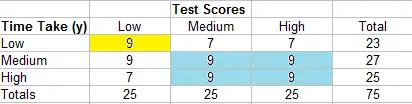
- Pase a la siguiente celda (7). Las dos celdas de abajo y a la derecha son 9 y 9.
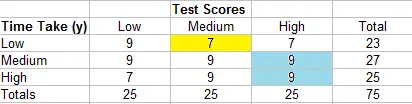
- Pase a la siguiente celda (7). No hay celdas a la derecha de esta celda.
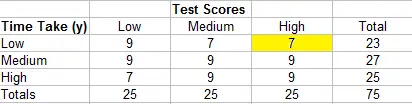
- Mover hacia abajo a la siguiente fila. La primera celda (9) tiene dos celdas a la derecha y abajo (9,9).
- Continúe hacia abajo en la tabla hasta que se hayan contabilizado todas las celdas.
El resumen de celdas para este ejemplo es:
- 9 (9 + 9 + 9 + 9) = 324
- 7 (9 + 9) = 126
- 7 (0) = 0
- 9 (9 + 9) = 162
- 9 (9) = 81
- 9 (0) = 0
- 7 (0) = 0
- 9 (0) = 0
- 9 (0) = 0
Sumándolos todos juntos, tenemos:
N c = 324 + 162 + 81 + 126 = 693
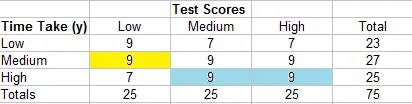
Encuentre el N d de la misma manera, solo que esta vez comience en la parte superior derecha y cuente todas las celdas a la izquierda y al final.
- 7 (9 + 9 + 7 + 9) = 238
- 7 (9 + 7) = 112
- 9 (0) = 0
- 9 (9 + 7) = 144
- 9 (7) = 63
- 9 (0) = 0
- 9 (0) = 0
- 9 (0) = 0
- 7 (0) = 0
Sumándolos todos juntos, tenemos:
N d = 238 + 112 + 144 + 63 = 557
Lo que significa que Gamma es:
(693 – 557) / (693 + 557) = 0,12
Prácticamente no hay significancia (0,12 es cercano a cero)
Pruebas de significancia
La prueba gamma de significancia funciona como la mayoría de las otras pruebas de hipótesis : encuentre una estadística de prueba y compárela con un valor de tabla. Paso por encima de los pasos aquí, por lo que si nunca ha realizado una prueba de hipótesis antes, puede leer este artículo: ¿Qué es la prueba de hipótesis?
La fórmula para el estadístico de prueba es: Insertando los valores del ejemplo 2 anterior, tenemos: = .4103
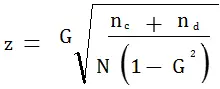
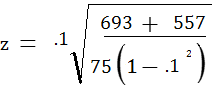
El valor de la tabla z (para un nivel alfa del 5 % ) es 1,96. (¿No está seguro de cómo leer una tabla z? Consulte: Cómo leer una tabla z ).
Z = .41 < Zcrit= ± 1.96
Como .41 es menor que el valor crítico z, no podemos rechazar la hipótesis nula de que hay una diferencia en las poblaciones.
Q de Yule
La Q de Yule es solo la versión 2 × 2 del coeficiente gamma. La fórmula es exactamente la misma, pero solo está usando las celdas a, b, c, d. Como nunca calculará más pares concordantes/discordantes que los que se encuentran en esas celdas, verá la fórmula escrita más comúnmente como:
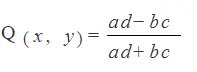
Fórmula Q de Yule
Para calcular la Q de Yule, siga los pasos del ejemplo simple de 2 × 2 anterior.
Relación de probabilidades y Q de Yule
La fórmula de la razón de probabilidades es (a*d) / (b*c). Una fórmula simple, usando la Q de Yule, convierte la razón de probabilidades a una escala de -1 a +1:
(O – 1) / (O + 1)
Interpretando la Q de Yule
La Q de Yule siempre es un número entre -1 y 1.
Q es 0: no hay asociación entre las variables.
Q = 0 a ± 0,29: una asociación despreciable o muy pequeña.
Q = -0,30 a -0,49 o 0,30 a 0,49: asociación moderada entre las variables.
Q = 0,50 y 0,69 o -0,50 y -0,69: asociación sustancial entre las variables.
Q > 0,70 o < -0,70: una asociación muy fuerte.
Si Q es 1 o -1, existe una asociación perfecta entre los eventos.
Una Q positiva apunta a una correlación positiva: si x es positiva, es probable que y también lo sea. Una Q negativa apunta a una correlación negativa: si x es positiva, es probable que y sea negativa.
Referencias
Bernard, H. Métodos de investigación social: enfoques cualitativos y cuantitativos. Recuperado el 10 de noviembre de 2017 de: https://books.google.com/books?id=VDPftmVO5lYC
Adeyemi, O. (2011) Medidas de Asociación para la Investigación en Planificación y Administración Educativas. Revista de investigación de matemáticas y estadística 3 (3): 82-90. Recuperado el 10 de noviembre de 2017 de: http://maxwellsci.com/print/rjms/v3-82-90.pdf
Medidas ordinales de
análisis de
correlación de pruebas de datos categóricos de asociación para datos ordinales. Recuperado el 3 de febrero de 2020 de: https://www.angelo.edu/faculty/ljones/gov3301/block14/objective4.htm

