Contenido de este artículo
Actualizado el 14 de marzo de 2022, por Luis Benites.
¿Qué es el Coeficiente Phi?
El Coeficiente Phi es una medida de asociación entre dos variables binarias (es decir, vivo/muerto, negro/blanco, éxito/fracaso). También se denomina Yule phi o Coeficiente de contingencia cuadrático medio y se utiliza para tablas de contingencia cuando:
- Al menos una variable es una variable nominal .
- Ambas variables son variables dicotómicas .
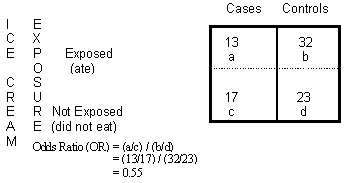
Una tabla de contingencia simple. Imagen: Departamento de Agricultura de Michigan
Para una tabla de contingencia de 2 × 2 donde a, b, c y d representan las frecuencias de observación (el conteo de celdas). La fórmula para phi es:
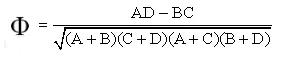
Ejemplo : encuentre phi para la siguiente tabla de contingencia: Solución : inserte los conteos en la fórmula y resuelva. Φ = ad – bc / √((a + b)(c + d)(a + c)(b + d)) Φ = 14*13 – 10*6 / √((14 + 10)(6 + 13 )(14 + 6)(10 + 13)) Φ = 182 – 60 / √((24)(19)(20)(23)) Φ = 122/ √((24)(19)(20)(23 )) Φ = 122/ 458 Φ = 0,266.
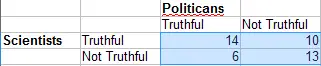
Interpretando el Coeficiente Phi
El coeficiente phi es una estadística simétrica , lo que significa que la variable independiente y las variables dependientes son intercambiables.
La interpretación del coeficiente phi es similar al coeficiente de correlación de Pearson. El rango es de -1 a 1, donde:
- 0 no es ninguna relación.
- 1 es una relación positiva perfecta: la mayoría de los datos se encuentran en las celdas diagonales.
- -1 es una relación negativa perfecta: la mayoría de sus datos no están en la diagonal.
El Departamento de Ciencias Políticas de la Universidad de Quinnipiac publicó esta útil lista del significado de los coeficientes de correlación de Pearson. La misma regla empírica se puede utilizar para el coeficiente Phi. Tenga en cuenta que estas son » estimaciones crudas » para interpretar las fortalezas de las relaciones.
| valor r = | |
| +.70 o superior | Relación positiva muy fuerte |
| +.40 a +.69 | Fuerte relación positiva |
| +.30 a +.39 | Relación positiva moderada |
| +.20 a +.29 | relación positiva débil |
| +.01 a +.19 | Relación nula o insignificante |
| 0 | Sin relación |
| -.01 a -.19 | Relación nula o insignificante |
| -.20 a -.29 | relación negativa débil |
| -.30 a -.39 | Relación negativa moderada |
| -.40 a -.69 | Fuerte relación negativa |
| -.70 o superior | Relación negativa muy fuerte. |
Referencias :
Universidad de Quinnipiac. Significado de Pearson. Recuperado el 20 de junio de 2016 de: http://faculty.quinnipiac.edu/libarts/polsci/Statistics.html
Yule, GU (1912). Estadista JR. Soc., 75,
576–642. (Sobre los métodos para medir la
asociación entre dos variables. La primera
identificación del coeficiente phi).
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
