Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 8 de junio de 2022, por Luis Benites.
Los árboles de probabilidad son útiles para calcular probabilidades combinadas para secuencias de eventos. Le ayuda a trazar gráficamente las probabilidades de muchas posibilidades, sin el uso de complicadas fórmulas de probabilidad.
Mire el video para ver un ejemplo.
Cómo dibujar un árbol de probabilidad Mira este video en YouTube .
¿No puedes ver el vídeo? Haga clic aquí
¿Por qué usar un árbol de probabilidad?
A veces no sabes si multiplicar o sumar probabilidades. Un árbol de probabilidad hace que sea más fácil saber cuándo sumar y cuándo multiplicar. Además, ver un gráfico de su problema, a diferencia de un montón de ecuaciones y números en una hoja de papel, puede ayudarlo a ver el problema con mayor claridad.
Partes de un diagrama de árbol de probabilidad
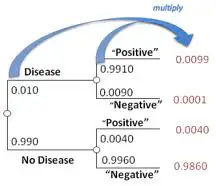
Un árbol de probabilidad tiene dos partes principales: las ramas y los extremos (a veces llamados hojas ). La probabilidad de cada rama generalmente se escribe en las ramas, mientras que el resultado se escribe en los extremos de las ramas. Los árboles de probabilidad de multiplicación y suma simplifican la cuestión de si multiplicar o sumar probabilidades: multiplique a lo largo de las ramas y sume probabilidades a lo largo de las columnas. En el siguiente ejemplo (de la Universidad de Yale), puede ver cómo sumando la columna de la derecha suma 1, que es lo que esperaríamos que fuera la suma total de todas las probabilidades: .9860 + 0.0040 + 0.0001 + 0.0099 = 1
Usos de la vida real
Los árboles de probabilidad no son solo una herramienta teórica que se usa en el aula: los científicos y estadísticos los usan en muchas ramas de la ciencia, la investigación y el gobierno. Por ejemplo, el gobierno federal utilizó el siguiente árbol como parte de un programa de alerta temprana para evaluar el riesgo de más erupciones en el Monte Pinatubo, un volcán activo en Filipinas.
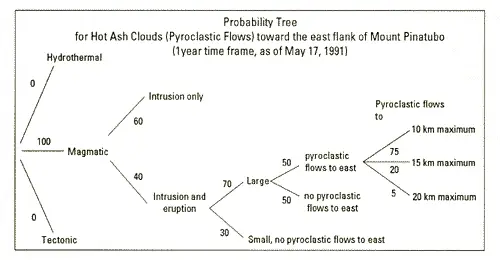
Imagen: USGS.
Cómo usar un árbol de probabilidad o un árbol de decisión
A veces, se enfrentará a una pregunta de probabilidad que simplemente no tiene una solución simple. Dibujar un árbol de probabilidad (o diagrama de árbol) es una forma de ver todas las opciones posibles y evitar cometer errores matemáticos. Esta guía le mostrará paso a paso el proceso de usar un árbol de decisión.
Cómo usar un árbol de probabilidad: Pasos
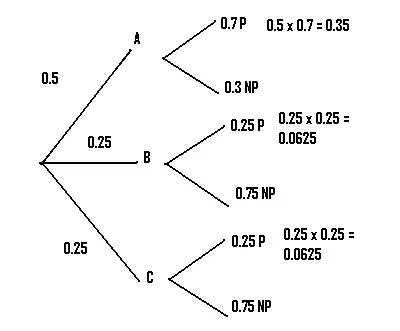
Pregunta de ejemplo : Un fabricante de aviones tiene tres fábricas AB y C que producen el 50 %, 25 % y 25 %, respectivamente, de un avión en particular. El setenta por ciento de los aviones producidos en la fábrica A son aviones de pasajeros, el 25% de los producidos en la fábrica B son aviones de pasajeros y el 25% de los aviones producidos en la fábrica C son aviones de pasajeros. Si se selecciona al azar un avión producido por el fabricante, calcule la probabilidad de que el avión sea un avión de pasajeros.
Paso 1: Dibuja líneas para representar el primer conjunto de opciones en la pregunta (en nuestro caso, 3 fábricas). Etiquételos: nuestra pregunta enumera AB y C, así que eso es lo que usaremos aquí.
Paso 2: Convierta los porcentajes a decimales y colóquelos en la rama correspondiente del diagrama. Para nuestro ejemplo, 50 % = 0,5 y 25 % = 0,25.
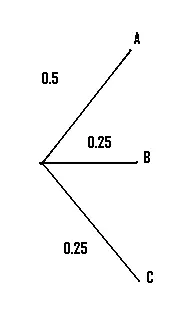
Paso 3: Dibuja el siguiente conjunto de ramas. En nuestro caso, nos dijeron que el 70% de la producción de la fábrica A era de pasajeros. Convirtiendo a decimales, tenemos 0.7 P («P» es solo mi abreviatura aquí para «Pasajero») y 0.3 NP («NP» = «No pasajero»).
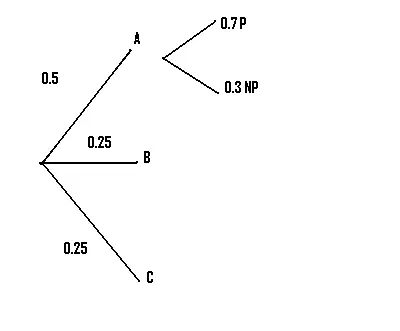 Paso 4: Repita el paso 3 para tantas sucursales como le indiquen .
Paso 4: Repita el paso 3 para tantas sucursales como le indiquen .
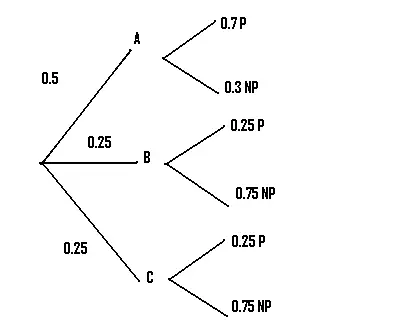 Paso 5: Multiplique las probabilidades de la primera rama que produce el resultado deseado en conjunto . En nuestro caso, queremos saber sobre la producción de aviones de pasajeros, por lo que elegimos la primera rama que conduce a P.
Paso 5: Multiplique las probabilidades de la primera rama que produce el resultado deseado en conjunto . En nuestro caso, queremos saber sobre la producción de aviones de pasajeros, por lo que elegimos la primera rama que conduce a P.
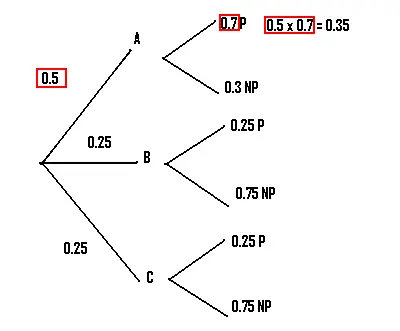
Paso 6: Multiplique las ramas restantes que den el resultado deseado. En nuestro ejemplo, hay dos ramas más que pueden conducir a P.
 Paso 6: sume todas las probabilidades que calculó en los pasos 5 y 6. En nuestro ejemplo, teníamos:
Paso 6: sume todas las probabilidades que calculó en los pasos 5 y 6. En nuestro ejemplo, teníamos:
.35 + .0625 + .0625 = .475
¡Eso es todo!
Ejemplo 2
Ejemplo de pregunta: Si lanzas una moneda al aire tres veces, ¿cuál es la probabilidad de obtener 3 caras? El primer paso es calcular la probabilidad de obtener cara lanzando la moneda una vez . La probabilidad es 0,5 (tienes un 50 % de probabilidad de sacar cara y un 50 % de probabilidad de sacar cruz). Esas probabilidades están representadas en los extremos de cada rama.
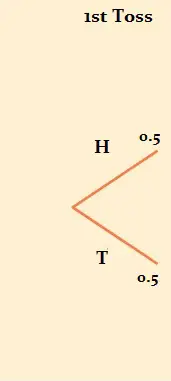
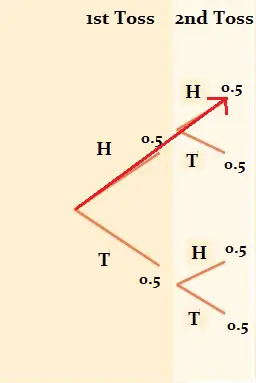 Luego, agregue dos ramas más a cada rama para representar el segundo lanzamiento de moneda. La probabilidad de obtener dos caras se muestra con la flecha roja. Para obtener la probabilidad, multiplica las ramas:
Luego, agregue dos ramas más a cada rama para representar el segundo lanzamiento de moneda. La probabilidad de obtener dos caras se muestra con la flecha roja. Para obtener la probabilidad, multiplica las ramas:
0,5 * 0,5 = 0,25 (25%).
Esto tiene sentido porque los posibles resultados de cara y cruz son HH, HT, TT o TH (cada combinación tiene una probabilidad del 25 %).
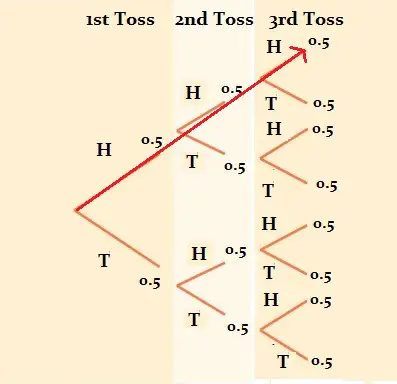 Finalmente, agregue una tercera fila (porque estábamos tratando de encontrar la probabilidad de sacar 3 caras ). Multiplicando a través de las ramas por HHH obtenemos:
Finalmente, agregue una tercera fila (porque estábamos tratando de encontrar la probabilidad de sacar 3 caras ). Multiplicando a través de las ramas por HHH obtenemos:
0.5 * 0.5 * 0.5 = 0.125, o 12.5%.
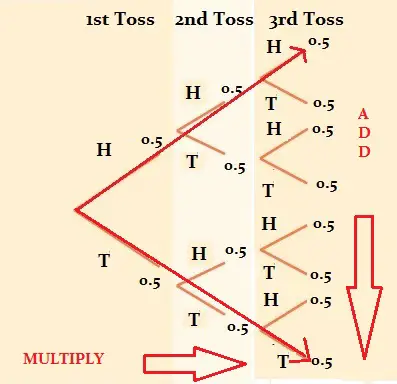 En la mayoría de los casos, multiplicarás las ramas para obtener probabilidades. Sin embargo, también puede querer sumar verticalmente para obtener probabilidades. Por ejemplo, si quisiéramos averiguar nuestra probabilidad de obtener HHH O TTT, primero calcularíamos las probabilidades para cada uno (0,125) y luego sumaríamos ambas probabilidades: 0,125 + 0,125 = 0,250.
En la mayoría de los casos, multiplicarás las ramas para obtener probabilidades. Sin embargo, también puede querer sumar verticalmente para obtener probabilidades. Por ejemplo, si quisiéramos averiguar nuestra probabilidad de obtener HHH O TTT, primero calcularíamos las probabilidades para cada uno (0,125) y luego sumaríamos ambas probabilidades: 0,125 + 0,125 = 0,250.
Sugerencia: puede verificar que dibujó el árbol correctamente sumando verticalmente: todas las probabilidades verticales deben sumar 1.
Siguiente : Diagrama de árbol Ejemplo de la vida real
Referencias
Punongbayan, R. et al. Repositorio de USGS: Evaluaciones y advertencias de peligro de erupción.
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
