Correlación parcial y semiparcial: definición y ejemplo

Actualizado el 3 de febrero de 2022, por Luis Benites.

¿Qué es la correlación parcial?

La correlación parcial mide la fuerza de una relación entre dos variables, mientras controla el efecto de una o más variables. Por ejemplo, es posible que desee ver si existe una correlación entre la cantidad de alimentos ingeridos y la presión arterial, mientras controla el peso o la cantidad de ejercicio. Es posible controlar múltiples variables (llamadas variables de control o covariables ). Sin embargo, generalmente no se recomienda más de uno o dos porque cuantas más variables de control, menos confiable es la prueba.

La correlación parcial tiene una variable independiente continua (el valor de x) y una variable dependiente continua (el valor de y); Esto es lo mismo que en el análisis de correlación regular. En el ejemplo anterior de presión arterial, la variable independiente es «cantidad de comida ingerida» y la variable dependiente es «presión arterial». Las variables de control (peso y cantidad de ejercicio) también deben ser continuas.

Notación

Un punto en el subíndice separa las variables correlacionadas y las variables controladas. Por ejemplo, la correlación entre la ingesta calórica (X ₁ ) y la presión arterial (X ₂ ), mientras se controla el peso (X ₃ ), se escribe como:
r _12.3
Alternativamente, se usa una barra en lugar de un punto y un subíndice: r(1, 2|3).

Ejecución de la prueba

El coeficiente de correlación, r, también se utiliza para mostrar los resultados de la correlación parcial. Al igual que el coeficiente de correlación regular, r _parcial devuelve un valor de -1 a 1.

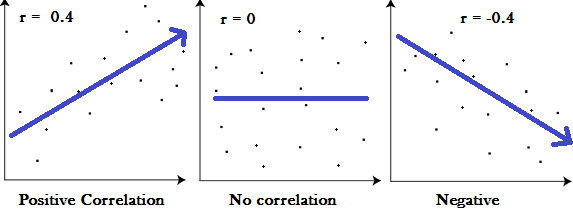
Gráficos que muestran una correlación de -1, 0 y +1

La correlación parcial generalmente se lleva a cabo ejecutando un análisis de regresión múltiple . Algunos programas de software incluyen correlación parcial. Por ejemplo, en SPSS , elija Analizar > Correlaciones > Parcial.

Cómo interpretar el resultado

Si la correlación parcial, r _12.3 , es menor que la correlación simple (dos variables) r ₁₂ , pero mayor que 0, entonces la variable 3 explica en parte la correlación entre X e Y.

Correlación semiparcial

La correlación semiparcial es casi lo mismo que la parcial. De hecho, muchos autores usan los dos términos para significar lo mismo. Sin embargo, otros hacen la siguiente distinción sutil:

Con la correlación semiparcial, la tercera variable se mantiene constante para X o Y, pero no para ambos ; con parcial, la tercera variable se mantiene constante tanto para X como para Y.

Por ejemplo, la estadística de correlación semiparcial puede decirnos la parte particular de la varianza que explica una variable independiente particular . Explica cómo una variable independiente específica afecta a la variable dependiente , mientras que otras variables se controlan para evitar que interfieran.

Para encontrarlo, calcula la correlación entre la variable dependiente y el residuo de la predicción de una variable independiente por las demás.

Ejemplo

Supongamos que usamos un conjunto de datos (de un artículo de 2002 de Abdi et al.) que enumera tres variables sobre seis niños. A cada niño se le evaluó la duración de la memoria (Y) y la velocidad del habla (X ₂ ), y también se anotó su edad. Se deseaba una estadística de correlación que predijera Y (lapso de memoria) a partir de X ₁ y X ₂ (edad y velocidad del habla).

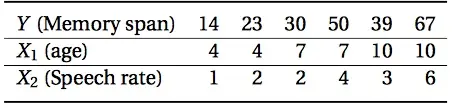
Normalmente, en una situación en la que X ₁ y X ₂ fueran variables aleatorias independientes , averiguaríamos la importancia de cada variable calculando un coeficiente de correlación al cuadrado entre X ₁ y X ₂ y la variable dependiente Y. Sabríamos que estas los coeficientes de correlación al cuadrado fueron iguales al coeficiente de correlación múltiplo al cuadrado. Pero en un caso como el nuestro, X ₁ y X ₂ son cualquier cosa menos independientes. La velocidad del habla depende en gran medida de la edad, por lo que usar el coeficiente cuadrático contará las contribuciones de cada variable varias veces.

Referencias

1. Abdi, Herve. Coeficientes de Regresión Parcial (Semi Parcial) y Parcial. Obtenido de https://www.utdallas.edu/~herve/Abdi-PartialRegressionCoficient2007-pretty.pdf el 8 de mayo de 2018
2. Abdi, H., Dowling, WJ, Valentín, D., Edelman, B. y Posamentier M. (2002). Diseño Experimental y métodos de investigación. Manuscrito no publicado. Richardson: Universidad de Texas en Dallas, Programa de Cognición.
3. Brannick, M. Correlación parcial y semiparcial. Recuperado de http://faculty.cas.usf.edu/mbrannick/regression/Partial.html el 8 de mayo de 2018
4. Sharpa, J. (2007). Estadísticas comerciales. Pearson Educación India.
5. Ayuda ESTADÍSTICA. Correlación semiparcial (o parcial). Obtenido de http://documentation.statsoft.com/STATISTICAHelp.aspx?path=glossary/GlossaryTwo/S/SemiPartialorPartCorrelation el 8 de mayo de 2018
6. Weatherburn, C. (1949). A Primer Curso Estadísticas Matemáticas . Archivo de la COPA.