Actualizado por ultima vez el 26 de marzo de 2022, por Luis Benites.
¿Qué es el factor de corrección de continuidad?
Un factor de corrección de continuidad se usa cuando usa una distribución de probabilidad continua para aproximar una distribución de probabilidad discreta . Por ejemplo, cuando desea utilizar la normal para aproximar un binomio .
Mira el video para ver un ejemplo:
Ejemplo de factor de corrección de continuidad 
Mira este video en YouTube .
¿No puedes ver el vídeo? Haga clic aquí.
De acuerdo con el teorema del límite central , la media muestral de una distribución se vuelve aproximadamente normal si el tamaño de la muestra es «suficientemente grande». por ejemplo, la distribución binomial se puede aproximar con una distribución normal siempre que n*p y n*q sean al menos 5. Aquí,
- n = cuántos artículos hay en su muestra,
- p = probabilidad de un evento (por ejemplo, 60%),
- q = probabilidad de que el evento no suceda (100% – p).
El factor de corrección de continuidad explica el hecho de que una distribución normal es continua y una binomial no lo es. Cuando usa una distribución normal para aproximar una distribución binomial, tendrá que usar un factor de corrección de continuidad. Es tan simple como sumar o restar .5 al valor discreto de x : usa la siguiente tabla para decidir si sumas o restas.
Tabla de factores de corrección de continuidad
¿ Necesitas ayuda con la mesa? ¡Mira nuestra página de tutoría!
- Si P(X=n) usa P(n – 0.5 < X < n + 0.5)
- Si P(X > n) usa P(X > n + 0.5)
- Si P(X ≤ n) use P(X < n + 0.5)
- Si P (X < n) use P (X < n – 0.5)
- Si P(X ≥ n) use P(X > n – 0.5)
Hagamos la tabla un poco más concreta usando x = 6 como ejemplo. La columna de la izquierda muestra lo que está buscando (por ejemplo, la probabilidad de que x = 6), mientras que la columna de la derecha muestra lo que le sucede a 6 después de aplicar el factor de corrección de continuidad.
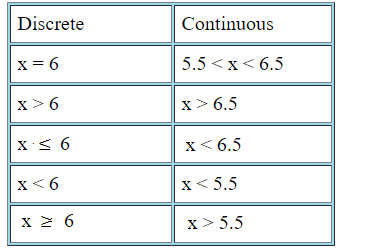
Ejemplo de factor de corrección de continuidad
El siguiente ejemplo muestra un problema resuelto en el que realmente usará el factor de corrección de continuidad para resolver un problema de probabilidad usando la tabla z .
Problema de ejemplo: si n = 20 y p = .25, ¿cuál es la probabilidad de que X ≥ 8?
Paso 1: Averigüe si el tamaño de su muestra es «suficientemente grande». Comience calculando n*p y n*q:
np = 20 * .25 = 5 (nota: esta es también la x̄ media
) nq = 20 * .75 = 15
Ambos están sobre 5, por lo que podemos usar la continuidad factor de corrección.
Paso 2: encuentre la varianza de la distribución binomial :
n*p*q = 20 * .25 * .75 = 3.75
Deje este número a un lado por un momento. Utilizará este valor en el paso 4 para encontrar una puntuación z.
Paso 3: Use el factor de corrección de continuidad en el valor X. Para este ejemplo, tenemos un signo mayor que o igual (≥), por lo que la tabla nos dice:
P(X ≥ n) use P(X > n – 0.5)
X ≥ 8 se convierte en X ≥ 7.5.
Paso 4: encuentre el puntaje z . Necesitará los tres valores de arriba:
- La media (x̄) del Paso 1,
- La(s) varianza(s) del Paso 2,
- El valor X i del Paso 3.
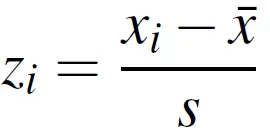
z = 7,5 – 5 / √3,75 = 1,29
Paso 5: Busque el Paso 4 en la tabla z .
1,29 = 0,4015.
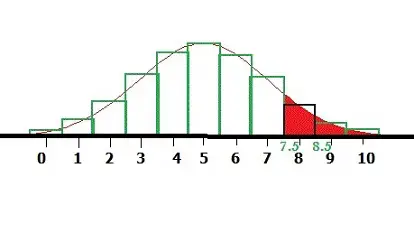
Paso 6: Resta el Paso de .5 para obtener el área (buscamos la cola derecha en la imagen de arriba):
.5 – .4015 = 0.0985.
La probabilidad de que X ≥ 8 es 0,0985.
¿Por qué se utiliza el factor de corrección de continuidad?
Mientras que la distribución normal es continua (incluye todos los números reales ), la distribución binomial solo puede tomar números enteros . La pequeña corrección es una concesión por el hecho de que está utilizando una distribución continua .
Una curva de distribución normal.
Echa un vistazo a nuestro canal de Youtube, donde encontrarás toneladas de videos para ayudarte con las estadísticas.
Referencias
Gonick, L. (1993). La guía de dibujos animados de estadísticas . Harper Perennial.
Kotz, S.; et al., editores. (2006), Enciclopedia de Ciencias Estadísticas , Wiley.
Vogt, WP (2005). Diccionario de estadística y metodología: una guía no técnica para las ciencias sociales . SABIO.
