Actualizado por ultima vez el 13 de septiembre de 2021, por Luis Benites.
Mire el video para obtener una descripción general y cómo encontrar la media de datos agrupados:
Datos agrupados frente a datos no agrupados 
Mira este video en YouTube .
¿No puedes ver el vídeo? Haga clic aquí
¿Qué son los datos agrupados?
Los datos agrupados son datos que se han agrupado en categorías. Se pueden utilizar histogramas y tablas de frecuencia para mostrar este tipo de datos:
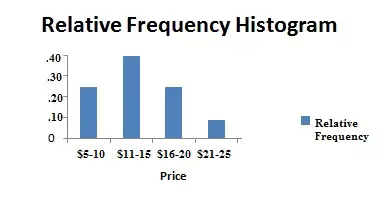
Histograma de frecuencia relativa que muestra las ventas de libros de un día determinado, ordenados por precio.
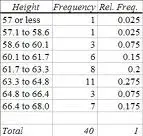
Una tabla de frecuencia que muestra datos agrupados por altura. Imagen: SHU.edu
Los datos se agrupan por clases o bins .
Datos agrupados frente a datos no agrupados
Los datos no agrupados son los datos que recopila por primera vez de un experimento o estudio. Los datos son sin procesar, es decir, no están ordenados en categorías, clasificados o agrupados de otra manera. Un conjunto desagrupado de datos es básicamente una lista de números.
Cálculo de la media muestral para datos agrupados
Cuando tiene una tabla de frecuencia u otro grupo de datos, el conjunto original de datos se pierde y se reemplaza con estadísticas para el grupo. No puede encontrar la media muestral exacta (ya que no tiene los datos originales), pero puede encontrar una estimación. La fórmula para estimar la media muestral para datos que han sido agrupados es:
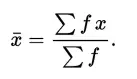
Ejemplo de pregunta: encuentre la media muestral para la siguiente tabla de frecuencias.
| Puntaje | Frecuencia ( f ) |
|---|---|
| Entre 5 y 10 | 1 |
| 10 ≤ t < 15 | 4 |
| 15 ≤ t < 20 | 6 |
| 20 ≤ t < 25 | 4 |
| 25 ≤ t < 30 | 2 |
| 30 ≤ t < 35 | 3 |
| TOTALES | 20 |
Paso 1: encuentre el punto medio para cada intervalo de clase. el punto medio es justo el medio de cada intervalo. Por ejemplo, la mitad de 10 y 15 es 12,5:
| Puntaje | Frecuencia ( f ) | Punto medio ( x ) |
|---|---|---|
| Entre 5 y 10 | 1 | 7.5 |
| 10 ≤ t < 15 | 4 | 12.5 |
| 15 ≤ t < 20 | 6 | 17.5 |
| 20 ≤ t < 25 | 4 | 22.5 |
| 25 ≤ t < 30 | 2 | 27.5 |
| 30 ≤ t < 35 | 3 | 32.5 |
| TOTALES | 20 |
Paso 2: Multiplica el punto medio (x) por la frecuencia (f):
| Puntaje | Frecuencia ( f ) | Punto medio ( x ) | Punto medio x * frecuencia f |
|---|---|---|---|
| Entre 5 y 10 | 1 | 7.5 | 7.5 |
| 10 ≤ t < 15 | 4 | 12.5 | 50 |
| 15 ≤ t < 20 | 6 | 17.5 | 105 |
| 20 ≤ t < 25 | 4 | 22.5 | 90 |
| 25 ≤ t < 30 | 2 | 27.5 | 55 |
| 30 ≤ t < 35 | 3 | 32.5 | 97.5 |
| TOTALES | 20 | 405 |
Sume todos los totales de este paso. En otras palabras, sume todos los valores de la última columna (debe obtener 405).
Paso 3: Divide la última columna (f*x) por la segunda columna (f):
La media (x̄) = 405 / 20 = 20,25.
Referencias
Agresti A. (1990) Análisis de datos categóricos. John Wiley and Sons, Nueva York.
Klein, G. (2013). La caricatura Introducción a la estadística. Colina y Wamg.
