Actualizado por ultima vez el 24 de noviembre de 2021, por Luis Benites.
En estadística, la desviación estándar es la forma habitual de medir la distancia desde la media o la mediana (técnicamente mide la dispersión o la varianza , que es una forma complicada de decir distancia).
Desviaciones absolutas y desviaciones promedio
Para comprender cuál es la desviación promedio , debe comprender qué es el término desviación absoluta . La desviación absoluta es la distancia entre cada valor en el conjunto de datos y la media o mediana de ese conjunto de datos. Para encontrar la distancia:
- Resta los valores. Por ejemplo, supongamos que la media de su conjunto de datos es 10 y tiene 5 valores: 1, 5, 10, 15 y 19. Las desviaciones absolutas son:
- 10 – 1 = 9
- 10 – 5 = 5
- 10 – 10 = 0
- 10 – 15 = -5
- 10 – 19 = -9
- Toma el valor absoluto de los números encontrados. El valor absoluto de -5 es 5 y -9 es 9. La lista final de valores sería 9, 5, 0, 5 y 9.
Tome todas estas desviaciones absolutas, encuentre el promedio y obtendrá la desviación promedio promedio.
Cómo calcular la desviación promedio
Los siguientes pasos muestran cómo calcular la desviación promedio de la media. Si desea calcular la desviación promedio de la mediana, simplemente reemplace cualquier valor de la media con el valor de la mediana.
La fórmula de desviación absoluta (es decir, la fórmula para calcular la distancia de un punto) es:
Desviación absoluta = |x – x̄|
Lo que lleva a la fórmula de desviación promedio:
D x = (|x 1 – x̄| + |x 2 – x̄| +…+ |x 3 – x̄|) / N
Si bien es simple, la fórmula nos crea problemas en el futuro, similar a cómo un valor absoluto dentro de una función puede causar problemas con la diferenciación . Además, la MAD muestral es un estimador sesgado de la MAD poblacional. En otras palabras, su valor promedio no coincide con las poblaciones MAD (Emory, 2021).
Pregunta de ejemplo: encuentre la desviación promedio del siguiente conjunto de números: 3, 8, 8, 8, 8, 9, 9, 9, 9.
Paso 1: encuentra la media:
(3 + 8 + 8 + 8 + 8 + 9 + 9 + 9 + 9) = 71,9 = 7,89.
Paso 2: Encuentra cada desviación absoluta individual usando la fórmula |x – x̄|.
- |3 – 7,89| = 4,89
- |8 – 7,89| = 0,11
- |8 – 7,89| = 0,11
- |8 – 7,89| = 0,11
- |8 – 7,89| = 0,11
- |9 – 7,89| = 1,11
- |9 – 7,89| = 1,11
- |9 – 7,89| = 1,11
- |9 – 7,89| = 1,11
Paso 3: Sume todos los valores que encontró en el Paso 1.
4.89+0.11+0.11+0.11+0.11+1.11+1.11+1.11+1.11= 9.77
Paso 4: Divida por la cantidad de elementos en su conjunto de datos. Hay 9 elementos, entonces:
9,77/9 = 1,09.
La desviación media es de 1,09.
Desviación estándar frente a desviación media
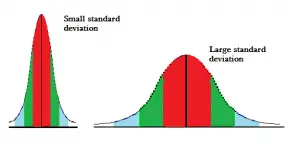
La desviación absoluta se usa con menos frecuencia que la desviación estándar , pero es extremadamente similar: ambas son una medida de dispersión. Hay ocasiones en las que dos conjuntos diferentes de datos con diferentes márgenes pueden producir exactamente la misma desviación absoluta. Sin embargo, la desviación estándar también puede ser la misma para diferentes conjuntos de datos. La desviación absoluta también se considera más precisa para situaciones de la vida real; algunos autores han sugerido que MAD debería reemplazar la desviación estándar para datos de la vida real. Además de ser potencialmente más preciso, también es mucho más simple de calcular.
¡ Visite nuestro canal de YouTube para ver cientos de videos de estadísticas básicas!
Referencias
Beyer, WH CRC Standard Mathematical Tables, 31ª ed. Boca Raton, FL: CRC Press, págs. 536 y 571, 2002.
Agresti A. (1990) Análisis de datos categóricos. John Wiley and Sons, Nueva York.
Emory, Universidad de Oxford (2021). http://mathcenter.oxford.emory.edu/site/math117/shapeCenterAndSpread/
Klein, G. (2013). La caricatura Introducción a la estadística. Colina y Wamg.
Vogt, WP (2005). Diccionario de estadística y metodología: una guía no técnica para las ciencias sociales . SABIO.
