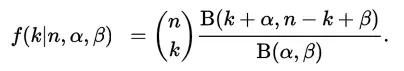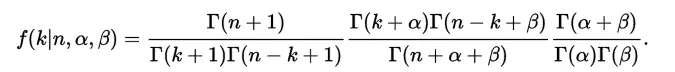Actualizado por ultima vez el 12 de mayo de 2022, por Luis Benites.
Una distribución binomial beta es una mezcla de distribución binomial y beta, por lo que puede resultarle útil leer estos artículos primero:
¿Qué es la Distribución Beta-Binomial?
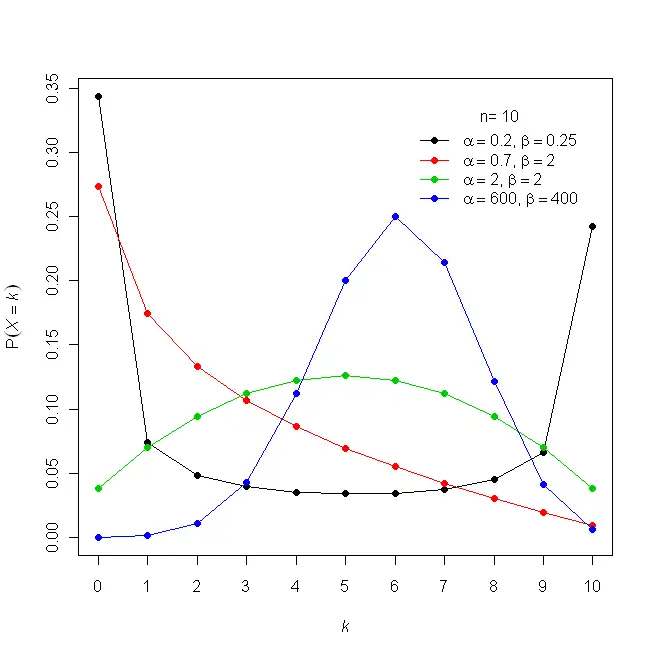
Función de densidad para varios valores de alfa y beta. Imagen: Mschuma|Wikimedia Commons.
La distribución binomial beta es uno de los modelos bayesianos más simples. Es ampliamente utilizado, incluso en epidemiología, pruebas de inteligencia y marketing.
Una distribución es beta-binomial si p, la probabilidad de éxito, en una distribución binomial tiene una distribución beta con parámetros de forma α > 0 y β > 0. Los parámetros de forma definen la probabilidad de éxito.
- Para valores grandes de α y β, la distribución se aproxima a una distribución binomial.
- Cuando α y β son iguales a 1, la distribución es igual a una distribución uniforme discreta de 0 a n.
- Cuando n = 1, la distribución es la misma que una distribución de Bernoulli.
Una diferencia importante entre una binomial y una binomial beta es que en una distribución binomial, p se fija para un número determinado de intentos; en un beta-binomial, p no es fijo y cambia de un ensayo a otro.
Derivación de la fórmula
Digamos que tiene m elementos en una prueba y cada elemento se prueba n veces. La fórmula de distribución binomial es:
P(X=x i ) = n C x i * P x i i * (1 – p i ) n – x i , i =1,2,3,…,n
Donde:
- P = probabilidad binomial,
- x i = número total de «éxitos» (aprobado o reprobado, cara o cruz, etc.) para la i -ésima prueba,
- p i = probabilidad de éxito en un ensayo individual,
- n = número de ensayos,
Quizás la forma más sencilla de pensar en el binomio beta es tomar la fórmula anterior y pensar en p como extraído aleatoriamente de una distribución beta.
Sin embargo, para escribir la fórmula en su totalidad, tome la función de densidad de probabilidad para la Distribución Beta: …y combínela con la fórmula de distribución binomial para obtener un pdf conjunto. Que también se puede escribir (usando las propiedades de distribución Beta) como:
![]()