Actualizado por ultima vez el 12 de mayo de 2022, por Luis Benites.
Se utiliza un modelo ARMA, o modelo de media móvil autorregresiva, para describir series temporales estocásticas débilmente estacionarias en términos de dos polinomios . El primero de estos polinomios es para autorregresión , el segundo para el promedio móvil .
A menudo, este modelo se denomina modelo ARMA(p,q) ; donde:
- p es el orden del polinomio autorregresivo,
- q es el orden del polinomio de la media móvil.
La ecuación viene dada por: Donde:
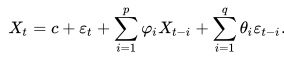
- φ = los parámetros del modelo autorregresivo,
- θ = los parámetros del modelo de promedio móvil.
- c = una constante,
- Σ = notación de suma ,
- ε = términos de error (ruido blanco).
Diferencia entre un modelo ARMA y ARIMA
Los dos modelos comparten muchas similitudes. De hecho, los componentes AR y MA son idénticos, combinando un modelo general autorregresivo AR(p) y un modelo general de promedio móvil MA(q). AR(p) hace predicciones usando valores previos de la variable dependiente . MA(q) realiza predicciones utilizando la media de la serie y los errores previos.
Lo que distingue a ARMA y ARIMA es la diferenciación . Un modelo ARMA es un modelo estacionario; Si su modelo no es estacionario, puede lograr la estacionariedad tomando una serie de diferencias. La “I” en el modelo ARIMA significa integrado; Es una medida de cuántas diferencias no estacionales se necesitan para lograr la estacionariedad. Si no hay diferencias involucradas en el modelo , entonces se convierte simplemente en un ARMA.
Un modelo con una d -ésima diferencia para ajustar y un modelo ARMA(p,q) se denomina proceso ARIMA de orden (p,d,q). Puede seleccionar p, d y q con una amplia gama de métodos, incluidos AIC , BIC y autocorrelaciones empíricas (Petris, 2009).
Otro modelo similar es ARIMAX, que es solo un ARIMA con variables explicativas adicionales .
Referencias
Petris, G. et al. (2009). Modelos lineales dinámicos con R . Springer Science & Business Media.

