Actualizado por ultima vez el 5 de marzo de 2022, por Luis Benites.
La distribución en serie de Edgeworth es una distribución de probabilidad continua que se aproxima a una distribución de probabilidad en términos de sus cumulantes y polinomios de Hermite . Relaciona la función de densidad de probabilidad (PDF) con una PDF de distribución normal estándar . A veces se ve en la teoría asintótica estadística, donde se calculan aproximaciones a las distribuciones estadísticas muestrales de orden mayor que n -1/2 [1].
La PDF para la distribución de la serie de Edgeworth bivariada (BVESD) es [2]
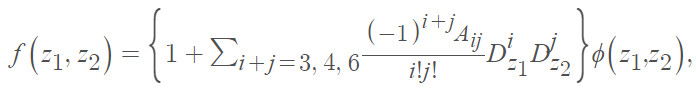
Donde
- φ(z 1 , z 2 ) es la función de densidad normal bivariada estándar,
- A ij son funciones de la población cumulantes, y
- D z1 , D z2 son operadores de derivadas parciales .
La función característica es:
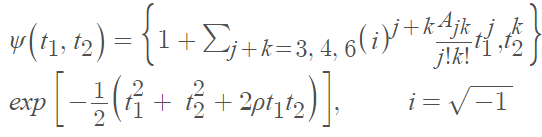
Es un desafío generar muestras a partir del PDF de la distribución de la serie Edgeworth. Además, la distribución de la probabilidad condicional de clasificación errónea para la ESD es intratable debido a la naturaleza compleja de la expresión. Relacionadas con la forma de distribución de Edgeworth están las expansiones de Cornish-Fisher, aunque no tiene una superioridad teórica general [3].
El ESD se ha utilizado para algunos fines prácticos, incluido el estudio de factores de carga de ráfagas no lineales (utilizados en el diseño de estructuras expuestas a vientos extremos) [4].
Referencias
[1] A. Adeyeye. Distribución asintótica de probabilidades de clasificación errónea para la distribución en serie de Edgeworth (ESD). Ingeniería Matemática. 2020; 4(1): 1-9 http://www.sciencepublishinggroup.com/j/engmath doi: 10.11648/j.engmath.20200401.11[2] S. Kocherlakota, K. Kocherlakota & N. Balakrishnan (1985) Efectos de la no normalidad sobre la parte para el coeficiente de correlación: distribución bivariada de series edgeworth, Journal of Statistical Computation and Simulation, 23:1-2, 41-51, DOI: 10.1080/00949658508810857
[3] Johnson, Kotz y Balakrishnan, (1994), Continuous Distribuciones Univariadas, Tomos I y II, 2do. Ed., John Wiley and Sons.

