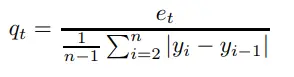Contenido de este artículo
Actualizado el 5 de marzo de 2022, por Luis Benites.
¿Qué es el error escalado absoluto medio?
El error escalado absoluto medio (MASE) es una métrica de error sin escala que proporciona cada error como una proporción en comparación con el error promedio de una línea de base.
Las ventajas de MASE incluyen que nunca da valores indefinidos o infinitos, por lo que es una buena opción para series de demanda intermitente (que surgen cuando hay períodos de demanda cero en un pronóstico). Se puede utilizar en una sola serie o como una herramienta para comparar múltiples series.
MASE se define mediante la siguiente ecuación:
MASE = media ( | q t | ) ~ Prestwich et. al, 2013
Donde:

- t = 1…n es el conjunto de períodos de muestra de pronóstico.
Comparación del error escalado absoluto medio con otras métricas
El error de escala absoluto medio (MASE) es una de las cuatro medidas principales de precisión de pronóstico. Los otros tres son:
- Métodos dependientes de la escala : p. ej. , error absoluto medio (MAE o MAD). Aunque estos son fáciles de calcular, no se pueden usar para comparar diferentes series debido a la dependencia de la escala.
- Métodos de porcentaje de error: por ejemplo , error porcentual absoluto medio (MAPE); Estos se pueden usar para comparar diferentes series porque son independientes de la escala. Sin embargo, no se pueden usar cuando tiene ceros en sus datos.
- Métodos de error relativo: promedia las tasas de error de una métrica elegida a la de una ingenua. Estas métricas no se pueden usar cuando tiene pequeños errores, porque los cálculos resultantes implicarían una división por cero.
Rob Hydman, en su artículo Foresight Otra mirada a las métricas de precisión de pronóstico para la demanda intermitente afirma que el error de escala absoluto medio es el único método de los cuatro que «… siempre da resultados sensatos». Sin embargo, Prestwich et. Tenga en cuenta que no puede usarlo cuando todas las demandas en la muestra son idénticas.
Referencias
Hyndman, R. (2006) Otra mirada a las métricas de precisión de pronóstico para la demanda intermitente.
Prestwich, S. et al. (2013). Medidas de error basadas en la media para la previsión de demanda intermitente. Recuperado el 29 de julio de 2019 de: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.741.9979&rep=rep1&type=pdf
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo: