Contenido de este artículo
Actualizado el 15 de agosto de 2021, por Luis Benites.
La distribución Gamma Poisson (GaP) es un modelo mixto con dos parámetros positivos, α y β.
Esta distribución jerárquica se utiliza para modelar una variedad de datos que incluyen tasas de falla, datos de secuenciación de ARN [1] y distribución aleatoria de microorganismos en una matriz alimentaria [2]. Cuando una distribución Gamma no se ajusta a los datos porque la distribución general de varias muestras está demasiado dispersa (es decir, la varianza es mayor que la media ), la distribución Gamma Poisson puede ser una buena opción.
PDF de distribución gamma de Poisson
La función de masa de probabilidad es [3]: Donde Γ denota la función gamma .
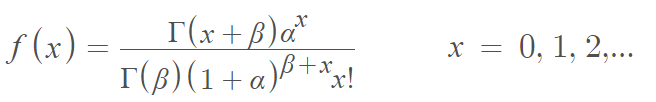
Conexión a la Distribución Binomial Negativa
La distribución binomial negativa puede surgir de una mezcla gamma de distribuciones de Poisson . Específicamente, esto puede suceder cuando la distribución de la densidad en las parcelas de muestra sigue una distribución gamma con parámetros dependientes de la escala y una media constante [4]. Quizás sea por esta razón que el proceso GaP a veces se denomina proceso binomial negativo [5], aunque técnicamente es más una forma de binomial negativo que su equivalente [6].
Referencias
[1] Holmes, S. & Huber, W. 4 Modelos de mezcla .[2] Toft, N. et al. El modelo Gamma-Poisson como método estadístico para determinar si los microorganismos se distribuyen aleatoriamente en una matriz alimentaria. Microbiología de los Alimentos. Volumen 23, Número 1, febrero de 2006, páginas 90-94.
[3] Distribución Gamma-Poisson. Recuperado el 8 de diciembre de 2021 de: http://www.math.wm.edu/~leemis/chart/UDR/PDFs/Gammapoisson.pdf
[4] Magnussen, S. (2008). Una distribución Gamma-Poisson del punto a la k distancia del evento más cercano. Ciencias Forestales 54(4): 429-441.
[5] Ewing, S. & Kunz, M. Ajuste de datos de tasa de fallas a la distribución Gamma-Poisson utilizando el método de momentos. Recuperado el 8 de enero de 2021 de: https://inldigitallibrary.inl.gov/sites/sti/sti/8059210.pdf
[6] Engelhardt, M. (1994). Eventos en el tiempo: análisis básico de datos de Poisson .
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
