Actualizado por ultima vez el 30 de mayo de 2022, por Luis Benites.
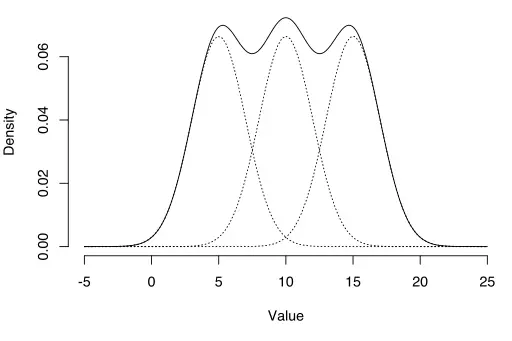
Un modelo de mezcla gaussiana.
Un modelo de mezcla gaussiana es una distribución ensamblada a partir de distribuciones gaussianas* multivariadas ponderadas. Los factores de ponderación asignan a cada distribución diferentes niveles de importancia. El modelo resultante es una superposición (es decir, una superposición) de curvas en forma de campana.
Los modelos de mezcla gaussiana son semiparamétricos . Paramétrico implica que el modelo proviene de una distribución conocida (que en este caso es un conjunto de distribuciones normales). Es semiparamétrico porque se pueden agregar al modelo más componentes, posiblemente de distribuciones desconocidas.
Usos
Los GMM se utilizan ampliamente para la estimación de densidad y agrupamiento en física . Sin embargo, tienen una amplia gama de aplicaciones en otros campos, como el modelado de observaciones meteorológicas en geociencias (Zi, 2011), ciertos modelos autorregresivos o el ruido de algunas series temporales .
Si cree que sus datos provienen de un conjunto de diferentes distribuciones normales, entonces el GMM es una herramienta de análisis adecuada. La distribución normal es una suposición subyacente , lo que significa que, si bien se supone que las distribuciones son gaussianas, es posible que no lo sean. En algunos casos, es posible que no pueda saberlo, pero use la lógica o el conocimiento previo para asumir que sus datos tienen una distribución normal. Por lo tanto, los modelos creados a partir de métodos GMM conllevan un cierto nivel de incertidumbre. Sin embargo, es fácil de usar (el software más popular tiene la capacidad de producir GMM) y, en comparación con el modelado no paramétrico , es relativamente simple.
En la mayoría de los casos, usará software para crear modelos de mezcla gaussiana. La agrupación, K-means e ISODATA se basan en el modelo de mezcla gaussiana.
La fórmula básica para un GMM con m componentes es:
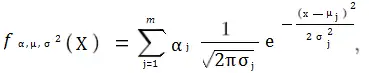
*Nota: En estadística, la distribución gaussiana se denomina distribución normal o curva normal. En las ciencias sociales, se llama curva de campana.
Referencias:
Li, Z. Aplicaciones del Modelo de Mezcla Gaussiana a las Observaciones Meteorológicas . IEEE Geoscience and Remote Sensing Letters (Volumen: 8, Número: 6, noviembre de 2011)
McLachlan, G. & Peel, D. (2000). Modelos de mezcla finita . Wiley-Interscience.
