Actualizado por ultima vez el 17 de enero de 2022, por Luis Benites.
En estadística, la función Q Q(x) generalmente se refiere a la función de distribución normal Φ(x). Para otros significados, consulte Otros usos.
La función Q de distribución normal Φ(x)
La función Q es solo uno menos la función de distribución acumulativa (CDF) para la distribución normal estandarizada . En otras palabras, te da el área de la cola correcta.
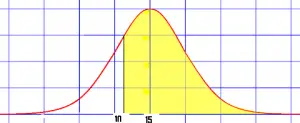
El área de una cola derecha en la distribución normal (área amarilla) se puede encontrar con la función Q.
La CDF para la distribución normal te da la probabilidad de que una variable aleatoria normal tome un valor igual o menor que x. La función Q es el complemento de esta; En otras palabras, es la probabilidad de que una variable aleatoria normal tome un valor mayor que x.
Como fórmula:
Q(x) = 1 – CDF = P(X > x)
La gráfica comienza con un área de 1, que representa el 100 % de probabilidad. En el punto más a la izquierda de la curva de campana, la «cola» derecha es en realidad el área completa de la curva.
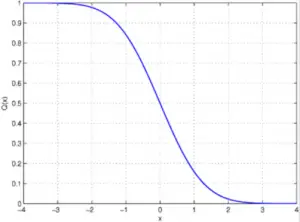
Gráfico de la función Q. El eje y representa las probabilidades de 0 a 1. El eje x representa las desviaciones estándar o puntuaciones z.
Calcular la función a mano es relativamente simple: encuentre la CDF y reste de uno. Algunos programas de software encuentran la función Q directamente. Por ejemplo, en MATLAB , la sintaxis es y = qfunc(x). Si su software no lo hace, encuentre el CDF y reste de uno.
Otros significados
Hay otros significados para la función Q, que incluyen:
- La log-verosimilitud esperada condicional , utilizada para calcular el paso E en el algoritmo EM (consulte Gupta y Chen 2011 para ver un ejemplo),
- El none q , una función especial usada en la teoría de funciones elípticas .
- Q-análogos y Q-series, utilizados en combinatoria y el estudio de funciones.
- Los q-productos Q n , donde n = 1,2,3.
- La función de partición Q , utilizada en termodinámica estadística.
- La función Marcum Q , que se utiliza principalmente en el procesamiento de señales.
Referencias
Gupta, M. y Chen, Y. (2011). Teoría y Uso del Algoritmo EM. Fundamentos y Tendencias en el Procesamiento de Señales. vol. 4, núm. 3 (2010) 223–296. Recuperado el 6 de diciembre de 2017 de http://www.mayagupta.org/publications/EMbookGuptaChen2010.pdf

