Actualizado por ultima vez el 26 de mayo de 2022, por Luis Benites.
Hay muchas distribuciones diferentes en forma de campana en las estadísticas. La más conocida es la “ curva de campana ”, formalmente llamada distribución normal . Sin embargo, la distribución normal no es la única distribución en forma de campana, hay otras, que incluyen:
- Distribución de la secante hiperbólica : miembro simétrico de la familia exponencial con una media de 0 y una varianza de 1. Es similar a la distribución normal tanto en forma como en simetría, pero la secante hiperbólica tiene colas ligeramente más pesadas [1].
- La distribución logística también se asemeja a una curva de campana; también tiene colas ligeramente más pesadas que la distribución normal. Aparece en regresión logística y redes neuronales feedforward [2].
- La distribución de Cauchy también tiene forma de campana, pero la media y la varianza no están definidas. La mediana viene dada por un parámetro de ubicación θ, y la dispersión viene dada por un parámetro de escala &simga;. La distribución de Cauchy se presenta como el cociente de dos variables aleatorias normales estándar independientes [2].
- Un modelo de mezcla gaussiana es una distribución de probabilidad compuesta por varias distribuciones gaussianas (normales) multivariadas ponderadas. El modelo es una superposición de curvas en forma de campana.
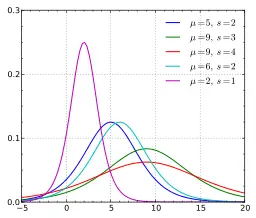
La distribución logística es una familia de distribuciones en forma de campana.
Propiedades de una distribución en forma de campana
Se nombra una distribución en forma de campana porque se parece a la forma de una campana cuando se traza en un gráfico. Estas distribuciones comparten varias propiedades importantes:
- Un solo pico en el centro (es decir, son distribuciones unimodales ).
- Simetría: si dibuja una línea vertical en el centro del gráfico, la mitad izquierda reflejará la derecha.
Referencias
PDF de la distribución logística. Imagen: Krishnavedala| Wikimedia Commons
[1] MJ Fischer, Distribuciones secantes hiperbólicas generalizadas, 1
SpringerBriefs in Statistics, DOI: 10.1007/978-3-642-45138-6_1
[2] Ross, G. Distribuciones de probabilidad/densidad.
[3] Cunningham, A. Patio de juegos de probabilidad: la distribución de Cauchy .

