Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 18 de octubre de 2022, por Luis Benites.
¿Qué es la Distribución Fréchet?
La distribución de Fréchet, también llamada distribución de valores extremos (EVD) Tipo II, se utiliza para modelar valores máximos en un conjunto de datos . Es uno de los cuatro EVD de uso común. Las otras tres son la Distribución Gumbel, la Distribución Weibull y la Distribución Generalizada de Valor Extremo . Esta distribución se utiliza para modelar una amplia gama de fenómenos como análisis de inundaciones, carreras de caballos, esperanza de vida humana, precipitaciones máximas y caudales de ríos en hidrología.
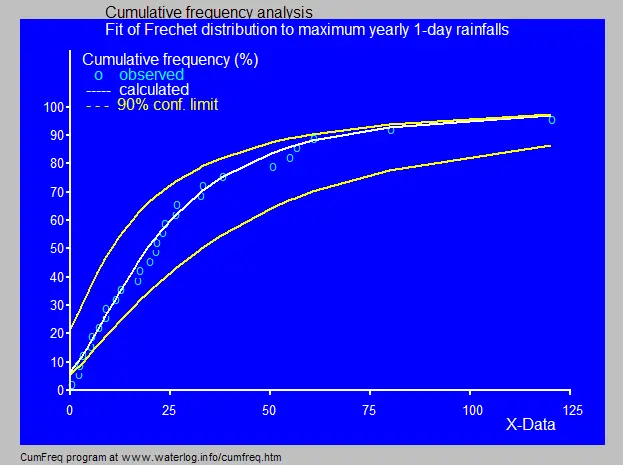
Precipitación extrema de un día modelada con la CDF de una Distribución Fréchet.
La CDF para la distribución de Fréchet es:
Pr(X≤x) = e -x -α .
La distribución de Fréchet tiene una larga cola de ley de potencia* que converge lentamente a 1. Tiene tres parámetros:
- Parámetro de forma , α,
- Parámetro de escala , β,
- Parámetro de ubicación , μ.
Algunos textos y programas usan una notación ligeramente diferente, aunque los principios subyacentes son los mismos. Por ejemplo, en algunos textos, los parámetros de forma, ubicación y escala se indican como ξ, m y α respectivamente. En R , los parámetros de forma, ubicación y escala se codifican como s, α y β.
La CDF general (que incluía los parámetros de ubicación y escala) es:
Pr(X ≤ x) = e-((x – μ)/β) α si x>μ.
Los parámetros de forma y escala pueden ser cualquier número real positivo y el parámetro de ubicación puede ser cualquier número real . Esto significa que la distribución está definida para el intervalo (μ, ∞).
Historia
La Distribución Fréchet lleva el nombre del matemático francés Maurice René Fréchet, quien la desarrolló en la década de 1920 como una distribución de valor máximo. Es igual al recíproco de la distribución de Weibull, pero se desarrollaron por separado. Fréchet pasó a describir una distribución similar a la de Weibull en 1927; Esto fue utilizado por Rosin y Rammler en 1933, quienes lo aplicaron para ajustarse a una distribución de tamaño de partículas. En 1951, Weibull tomó la distribución inversa de Fréchet , escribió un artículo en profundidad sobre ella y tomó su nombre.
Nota : *Según Sornette (2003), cualquier PDF con una cola que cae como una ley de potencia X -1-μ para X → +∞ tendrá su distribución de valor extremo convergente a Fréchet con α=1/μ.
Referencias :
- Fréchet, Maurice (1927), “Sur la loi de probabilité de l’écart maximum”, Annales de la Société Polonaise de Mathematique, Cracovie 6: 93–116.
- colofonia, P.; Rammler, E. (1933), “Las leyes que rigen la finura del carbón en polvo”, Revista del Instituto de Combustible 7: 29–36.
- Sornette, D. 2003. Fenómenos críticos en ciencias naturales: caos, fractales, autoorganización.
- Weibull, W. (1951), «Una función de distribución estadística de amplia aplicabilidad» (PDF), J. aplicación Mec.-Trans. ASME 18 (3): 293–297.
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
