Actualizado por ultima vez el 25 de noviembre de 2021, por Luis Benites.
La distribución de Irwin-Hall ( Uniform Sum Distribution ) es la distribución de la suma de n valores tomados de la distribución uniforme U(0, 1). Es similar a la distribución de Bates , que es la distribución de la media de n valores. La distribución lleva el nombre de dos demostraciones, dadas por Irwin (1927) y Hall (1927).
Esta distribución tiene muchas aplicaciones en matemáticas aplicadas, en parte debido a su simplicidad . Por ejemplo, las sumas de variables aleatorias deben calcularse en problemas relacionados con:
- Agregación de valores escalados con cifras significativas variables,
- Análisis de puntos de cambio,
- Datos extraídos de mediciones con diferentes niveles de precisión (Batsyn & Kalyagin, 2012).
Para n pequeño , la distribución es muy simple y sigue una distribución uniforme ( n = 1) o una distribución triangular ( n = 2). Puede dar aproximaciones spline a distribuciones normales (Marengo, 2017).
PDF de la distribución de Irwin-Hall
La función de densidad de probabilidad (PDF) de la distribución de Irwin-Hall viene dada por (Florescu, 2014): Donde signo(x) es la función de signo .
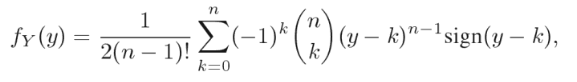
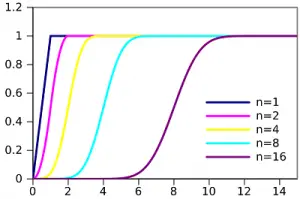
PDF para varios valores de n para la distribución de Irwin-Hall. Imagen: Thomasda|Wikimedia Commons.
Media, Varianza y Curtosis
La media de la distribución de Irwin-Hall es n /2 y la varianza es n /12. Las distribuciones de Irwin-Hall son platicúrticas ; Para n grande, la curtosis es cercana a 3 (Marengo, 2017).
Referencias
Batsyn, M. y Kalyagin, V. (2012). Una expresión analítica para la distribución de la suma de variables aleatorias con una densidad uniforme mixta y una función de masa.
Florescu, I. (2014). Probabilidad y Procesos Estocásticos 1ra Edición . Wiley.
Flury, B. Un primer curso de estadística multivariante (Springer Texts in Statistics) Edición de 1997.
Pasillo, P. (1927). La distribución de medias para muestras de tamaño n extraídas de una población en la que
la variable toma valores entre 0 y 1, siendo todos estos valores igualmente probables. biometrika,
vol. 19, núm. 3/4. págs. 240–245. Irwin J. (1927). Sobre la distribución de frecuencias de las medias de muestras de una población que tiene cualquier ley de frecuencia con momentos finitos, con especial referencia al tipo II de Pearson.
Biometrika, vol. 19, núm. 3/4. págs. 225–239.
Marengo, J et al. (2017). Una derivación geométrica de la distribución de Irwin-Hall . Revista Internacional de Matemáticas y Ciencias Matemáticas.

