Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 24 de agosto de 2021, por Luis Benites.
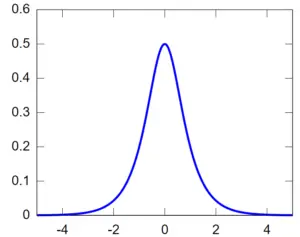
PDF de la distribución secante hiperbólica.
La distribución de la secante hiperbólica es un miembro simétrico en forma de campana de la familia exponencial con una media de 0 y una varianza de 1. Es una distribución continua que es tratable , lo que significa que el cálculo de la distribución en cualquier punto requiere tiempo polinomial .
PDF de distribución de la secante hiperbólica
Una variable aleatoria X = ln|Y 1 /Y 2 | sigue una distribución secante hiperbólica (donde Y son variables aleatorias normales). La densidad de la distribución es proporcional a la función secante hiperbólica, el recíproco de la función coseno hiperbólico definida por [1]:
cosh(x) = 0.5 [e x + e -x ]
La función de densidad de probabilidad de la secante hiperbólica es [2]: Donde μ ∈ ℝ y σ > 0 y
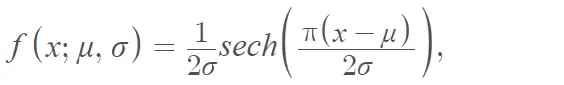
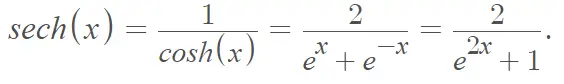
La media muestral y la mediana muestral son estimadores igualmente eficientes para la distribución de la población .
La distribución de la secante hiperbólica no es tan conocida como otras distribuciones familiares exponenciales debido a su aislamiento de muchos modelos estadísticos conocidos [3]. Tiene algunas similitudes con la distribución normal tanto en forma como en simetría. Ambas distribuciones tienen una densidad proporcional a sus funciones características aunque la secante hiperbólica tiene colas ligeramente más pesadas [4].
Referencias
Imagen superior: IkamusumeFan,
[1] Stat 5601 (Geyer) Distribución de secante hiperbólica. Recuperado el 18 de diciembre de 2021 de: https://www.stat.umn.edu/geyer/old02/5601/examp/hsec.html
[2] Rubio, F. The Hyperbolic Secant Distribution. Recuperado el 18 de diciembre de 2021 de: https://rpubs.com/FJRubio/HSD
[3] Ding, P. (2014). Tres Ocurrencias de la Distribución Hiperbólica-Secante. Recuperado el 18 de diciembre de 2021 de: https://arxiv.org/abs/1401.1267
[4] MJ Fischer, Generalized Hyperbolic Secant Distributions, 1
SpringerBriefs in Statistics, DOI: 10.1007/978-3-642-45138-6_1
Redactor del artículo
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
