Distribución Triangular / Distribución Triangular: Definición

Actualizado el 18 de octubre de 2021, por Luis Benites.

¿Qué es una distribución triangular?

Una distribución triangular (a veces llamada distribución triangular) es una distribución de probabilidad continua con forma de triángulo. Se define por:

• a: el valor mínimo , donde a ≤ c,
• c: el valor máximo (la altura del triángulo), donde a ≤ c ≤ b,
• b: el valor máximo , donde b ≥ c.

Esto hace que sea muy fácil estimar los parámetros de distribución a partir de datos de muestra:

• Utilice el mínimo muestral como estimador de a,
• Use el máximo de la muestra como un estimador para b, y
• Utilice cualquier estadística razonable (p. ej., la media muestral , la moda o la mediana ) como estimador de c.

Si no tiene datos de muestra , se puede usar el conocimiento experto para estimar un valor mínimo, máximo y más probable probable (es decir, la moda).

Los tres parámetros, ab y c, cambian la forma del triángulo: como todas las distribuciones de probabilidad, el área bajo la curva es 1. Por lo tanto, cuanto mayor sea la distancia entre a y c (es decir, el rango ), menor será la altura.

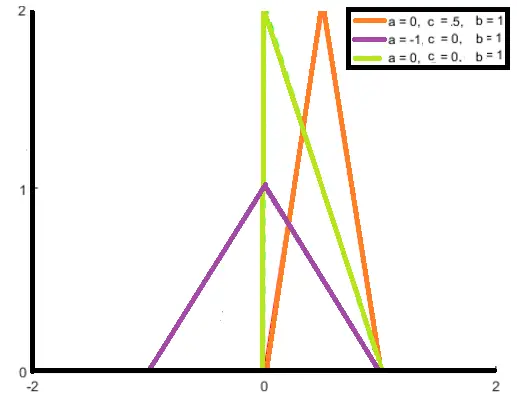
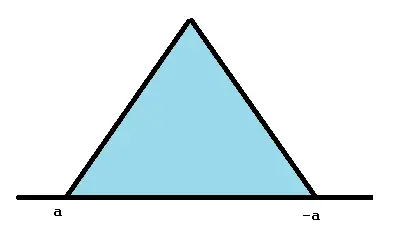
Cuando el pico está centrado en cero y a = b, se denomina distribución triangular simétrica . Cuando esto sucede, ayb son iguales pero de signo opuesto (p. ej., -2, 2) y, a veces, se denominan -a y a en lugar de a y b.

PDF, media y desviación estándar

La función de densidad de probabilidad , que se usa para encontrar la probabilidad de que una variable aleatoria caiga dentro de cierto rango, está dada por:

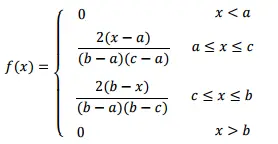
La media de esta distribución es:
μ = 1/3 (a + b + c).

La desviación estándar , s, es:
s = (1/√6) a.
Esta fórmula asume que la distribución está centrada en cero y que se conocen los puntos finales .

Referencia :
Samuel Kotz, S y van Dorp.J. (2004) Más allá de Beta. Capítulo de muestra sobre la distribución triangular disponible aquí de World Scientific.