Actualizado por ultima vez el 8 de septiembre de 2021, por Luis Benites.
La eficiencia de Pareto es una cualidad de las asignaciones en economía y teoría de juegos. Si una asignación es eficiente en el sentido de Pareto, ninguna opción puede mejorar sin empeorar al menos otra opción.
Es importante tener en cuenta que una asignación eficiente en el sentido de Pareto, si bien siempre es la más eficiente, no es necesariamente la mejor o la más justa . Una asignación puede ser muy injusta y muy desigual sin dejar de ser eficiente en el sentido de Pareto.
Por lo general, hay más de una asignación eficiente de Pareto. El conjunto de todas las asignaciones eficientes de Pareto se denomina frontera de Pareto, frente de Pareto o conjunto de Pareto. La siguiente imagen muestra varias opciones eficientes de Pareto como puntos rojos; Los puntos grises no son eficientes en el sentido de Pareto:
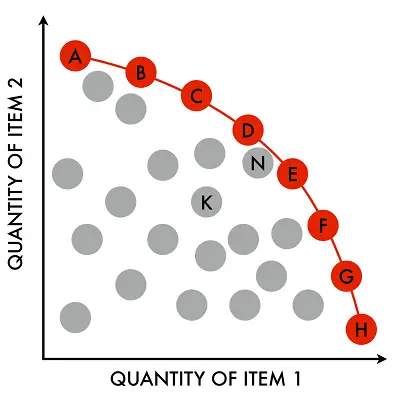
Un cambio en una asignación que mejora a un individuo sin dejar a nadie peor se denomina mejora de Pareto . Una vez que no se pueden realizar más mejoras de Pareto en una asignación, es por definición eficiente en el sentido de Pareto.
Ejemplos de eficiencia de Pareto
Suponga que tiene dos hijos, Donald y Mary, y ambos manejan sus dos negocios de frutas y dulces. Mary prefiere pasar la mayor parte del tiempo en el negocio de la fruta, especialmente en los huertos de manzanas; Donald prefiere manejar el negocio de los dulces.
Ahora suponga que expandió los negocios; otro tipo de manzana y otro tipo de barra de chocolate. Mary estaría feliz si le diera ambos; si las dos expansiones (manzana, caramelo) forman una fila ordenada, su asignación ideal sería (M, M). Su próxima asignación preferida sería (M, D); ella tendría las nuevas manzanas y Donald tendría los nuevos dulces.
Donald, semejanza, le encantaría todo (D, D). Si tuviera que regalarle algo a su hermana, elegiría las manzanas; por lo que su próxima asignación preferida también sería (M, D).
En este escenario (M, M) (D, D) y (M, D) son asignaciones eficientes en términos de Pareto. Hacer que Mary o Donald sean más felices en cualquiera de esos escenarios implicaría hacer que el otro sea menos feliz.
(D, M) por otro lado, es un ejemplo de una asignación que es Pareto ineficiente. Hacer que los dos niños intercambien productos sería una manera fácil de hacerlos más felices a los dos a la vez.
Es fácil ver aquí que Pareto eficiente no es igual a justo. Sin embargo, también puede ver que la asignación más justa y la eficiente en el sentido de Pareto no están en conflicto, porque una asignación que no es eficiente en el sentido de Pareto puede mejorar para todos los involucrados al realizar una mejora en el sentido de Pareto. La asignación más justa y mejor siempre se puede elegir del conjunto de Pareto.
Referencias
Nehring, Klaus. Folleto de clase Econ 100: Asignaciones eficientes en términos de Pareto
Obtenido de http://faculty.econ.ucdavis.edu/faculty/nehring/teaching/econ100-bluff/econ100-pareto.pdf el 2 de marzo de 2018Osborne, Martin. Eficiencia de Pareto
Obtenido de https://www.economics.utoronto.ca/osborne/2×3/tutorial/PE.HTM el 2 de marzo de 2018
Notas de clase de la Universidad de Chicago: Conceptos de Pareto
Obtenido de http://home.uchicago. edu/bdm/pepp/pareto.pdf el 2 de marzo de 2018
