Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 23 de octubre de 2021, por Luis Benites.
Es posible que desee leer este artículo primero: ¿Qué es la multicolinealidad?
¿Qué es un factor de inflación de varianza?
Un factor de inflación de varianza (VIF) detecta la multicolinealidad en el análisis de regresión . La multicolinealidad es cuando hay correlación entre predictores (es decir , variables independientes ) en un modelo; su presencia puede afectar negativamente los resultados de su regresión. El VIF estima cuánto se infla la varianza de un coeficiente de regresión debido a la multicolinealidad en el modelo.
Los VIF generalmente se calculan mediante software, como parte del análisis de regresión. Verá una columna VIF como parte de la salida. Los VIF se calculan tomando un predictor y retrocediéndolo contra todos los demás predictores del modelo. Esto le da los valores de R-cuadrado , que luego se pueden conectar a la fórmula VIF. «i» es el predictor que está viendo (por ejemplo, x 1 o x 2 ):
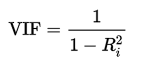
Interpretación del factor de inflación de la varianza
Los factores de inflación de la varianza van desde 1 en adelante. El valor numérico para VIF le dice (en forma decimal) qué porcentaje se infla la varianza (es decir, el error estándar al cuadrado) para cada coeficiente. Por ejemplo, un VIF de 1,9 le dice que la varianza de un coeficiente en particular es un 90 % mayor de lo que esperaría si no hubiera multicolinealidad, si no hubiera correlación con otros predictores.
Una regla general para interpretar el factor de inflación de la varianza:
- 1 = no correlacionado.
- Entre 1 y 5 = moderadamente correlacionado.
- Mayor que 5 = altamente correlacionado.
Exactamente qué tan grande debe ser un VIF antes de que cause problemas es un tema de debate. Lo que se sabe es que cuanto más aumente su VIF, menos confiables serán los resultados de su regresión. En general, un VIF superior a 10 indica una alta correlación y es motivo de preocupación. Algunos autores sugieren un nivel más conservador de 2,5 o superior.
A veces, un VIF alto no es motivo de preocupación en absoluto. Por ejemplo, puede obtener un VIF alto al incluir productos o potencias de otras variables en su regresión, como x y x 2 . Si tiene VIF altos para variables ficticias que representan variables nominales con tres o más categorías, eso no suele ser un problema.
Referencias
Esquivar, Y. (2008). La Enciclopedia Concisa de Estadística . Saltador.
Everitt, BS; Skrondal, A. (2010), The Cambridge Dictionary of Statistics , Cambridge University Press.
Redactor del artículo
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
