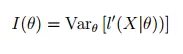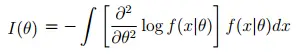Contenido de este artículo
Actualizado el 14 de febrero de 2022, por Luis Benites.
¿Qué es la información de Fisher?
La información de Fisher nos dice cuánta información sobre un parámetro desconocido podemos obtener de una muestra . En otras palabras, nos dice qué tan bien podemos medir un parámetro, dada una cierta cantidad de datos. Más formalmente, mide la cantidad esperada de información proporcionada por una variable aleatoria (X) para un parámetro (Θ) de interés. El concepto está relacionado con la ley de la entropía , ya que ambas son formas de medir el desorden en un sistema (Friedan, 1998).
Los usos incluyen:
- Describir el comportamiento asintótico de las estimaciones de máxima verosimilitud .
- Cálculo de la varianza de un estimador .
- Encontrar anteriores en la inferencia bayesiana.
Encontrar la información de Fisher
Encontrar la cantidad esperada de información requiere cálculo . Específicamente, se requiere una buena comprensión de las ecuaciones diferenciales si desea derivar información para un sistema.
Tres formas diferentes pueden calcular la cantidad de información contenida en una variable aleatoria X:
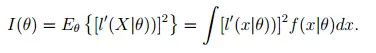
- Esto se puede reescribir (si cambia el orden de integración y diferenciación ) como:

- O, dicho de otra manera:

La ecuación inferior suele ser la más práctica. Sin embargo, es posible que no tenga que usar calculus , porque la información esperada ya se calculó para una gran cantidad de distribuciones. Por ejemplo:
- Ly et.al (y muchos otros) afirman que la cantidad esperada de información en una distribución de Bernoulli es:
I(Θ) = 1 / Θ (1 – Θ). - Para distribuciones mixtas , tratar de encontrar información puede “volverse bastante difícil” (Wallis, 2005). Si tiene un modelo mixto, el libro de Wallis Inferencia estadística e inductiva por longitud mínima de mensaje brinda un excelente resumen de los problemas que podría esperar.
Si está tratando de encontrar la información esperada, intente primero una búsqueda en Internet o en una base de datos académica: la solución para muchas distribuciones comunes (y muchas poco comunes) probablemente esté disponible.
Ejemplo
Encuentre la información de Fisher para X ~ N(μ, σ 2 ). El parámetro, μ, es desconocido.
Solución :
Para −∞ < x < ∞: Las derivadas primera y segunda son: Por lo tanto, la información de Fisher es:
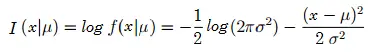
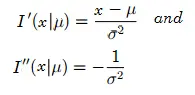
![]()
Otros usos
La información de Fisher se usa para propósitos ligeramente diferentes en las estadísticas bayesianas y la longitud mínima de descripción (MDL):
- Estadísticas bayesianas : encuentra una prioridad predeterminada para un parámetro.
- Longitud mínima de descripción (MDL) : mide la complejidad para diferentes modelos.
Referencias :
Frieden y Gatenby. (2010). Análisis exploratorio de datos usando FI. Medios de comunicación de ciencia y negocios de Springer.
Friedan (1998). Física de la información de Fisher: una unificación. Prensa de la Universidad de Cambridge.
Lehman, EL y Casella, G. (1998). Teoría de la estimación puntual (2ª edición). Nueva York, NY: Springer.
Ly, A. et. Alabama. Un tutorial sobre Fisher I. Recuperado el 8 de septiembre de 2016 de: http://www.ejwagenmakers.com/submitted/LyEtAlTutorial.pdf.
Wallis, C. (2005). Inferencia Estadística e Inductiva por Longitud Mínima de Mensaje. Medios de comunicación de ciencia y negocios de Springer.
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo: